自主招生与竞赛中的解析几何问题与普通高考中的解析几何问题在解法上并没有什么本质上的不同，最大的区别是增加了知识的综合性，包含的知识点多，而且知识的跨度比较大；另一方面，是在思维的灵活性、深刻性方面更高一些．

例1 横、纵坐标都是有理数的点叫有理点．求过的所有直线中，过两个不同的有理点的直线有几条．

【分析】本题若从解析几何角度看，思路很简单，就是先假设过的直线经过两个“有理点”，然后利用三点共线，看看有几组不同的解即可．所以，在这里，解析几何知识只是载体，重点考查的还是整数和有理数的性质．简答如下：

设，，其中均为有理数，

则过A，B两个有理点的直线方程为，

由于点在直线AB上，所以，

将上式整理，得，因为均为有理数，

只有当时，由于，所以，故只有一条．

例2 横、纵坐标都是整数的点叫整点．求平面上整点到直线距离的最小值．

【分析】设整点到直线距离为，

问题转化为：求m，n为整数时，的最小值．

由于，

所以，显然，只有当时，d取得最小值．

问题是时，能等于吗？

显然，时满足．

所以，我们可以断定，当，时，d取得最小值．

当然，如果知道如下结论问题的答案来得更快一些．

定理：方程（，）有解，若，

则

由于，所以

，即，时取得最小值．

例3从椭圆外一点向椭圆引两条切线，切点分别为A，B，求直线AB的方程．

【分析】我们知道，过圆上一点的切线方程为，

如果我们做变换，令，则椭圆方程变为，变为，那么圆在处的切线为，将

代入，得．

设，，则过A，B处的切线方程为，，

由于在两条切线上，所以且，

可见，的坐标满足方程，

所以过，的直线方程为．

【小结】本解法如果一味地通过计算获得结论未尝不可，但这不能体现数学的思维价值．本题在明确问题的基础上，通过“设而不求”以及对数学知识本质理解，顺利解决了相关问题，解题过程简洁优美．

例4 （2011清华大学）

抛物线的焦点为F，原点为O，直线AB经过点F，抛物线的准线与x轴交于点C，若,则

A． B． C． D．

【分析】

思路1本题按照常规思路是，抛物线是确定的，直线也是确定的，所以所求角是确定的，正切值也是确定的．

为了更具一般性，设抛物线方程是，过点的直线AB与抛物线交于A，B两点，不妨设点A在第一象限，且，（如图），

直线AB的方程为，则

联立，得，由于，所以，．

设，，则，，

，

又，所以，

整理，利用根与系数关系化简，得，

这是一个意想不到的、漂亮的结论，结果是一个与抛物线本身无关的定值，只与直线的斜率有关．

思路2 受到上述思路的启发，可以先进行几何要素关系的分析，再结合抛物线的定义，可以使得运算过程大为缩减．

过点A分别作x，y轴的垂线，垂足为分别是M，N，记直线AB的倾斜角为，则

在三角形AMF中，,

根据抛物线的定义，,

，

同理，，

即，

例5 （上海交大）对于两条垂直的直线和一个椭圆，已知椭圆无论如何滑动都与两条直线相切，求椭圆中心的轨迹．

解法1

以两条垂直的直线作为x，y轴建立直角坐标系．设椭圆长轴为2a，短轴为2b，

中心M（x0,y0）,则

关于切线轴对称的点为，

又，得

同理，关于切线轴对称的点为，

又，得

（1）+（2）得

由于每个象限对称，所以

解法2

将椭圆固定，作椭圆互相垂直的切线，这时，就没有“中心”了．但轨迹的本质是动点到两条垂直的直线距离之间的关系．

设椭圆方程为，

两个切点

两条切线为，

根据两条切线垂直，得①

设椭圆中心到切线的距离分别为，则

，，解出②

即，解出③

将②、③代入①2得，

又

所以

例6（2013华约试题）

设，在直线与上分别取点与,使且

，其中O是坐标原点．记AB中点M的轨迹为C．

（Ⅰ）求C的方程；

（Ⅱ）若抛物线与C在两点相切，证明两个切点分别在两条定直线上，并求在这两切点处的切线方程．

设，，，

由，得，

又，，

，

得曲线C：，双曲线

，

由，得，此时，

得，所以两切点在直线上，

，

求出切线即可．

例7（2014华约）

已知椭圆与圆，过椭圆上一点P做圆的两条切线，切点弦所在直线与x轴、y轴分别交于点E，F，求三角形OEF面积的最小值．

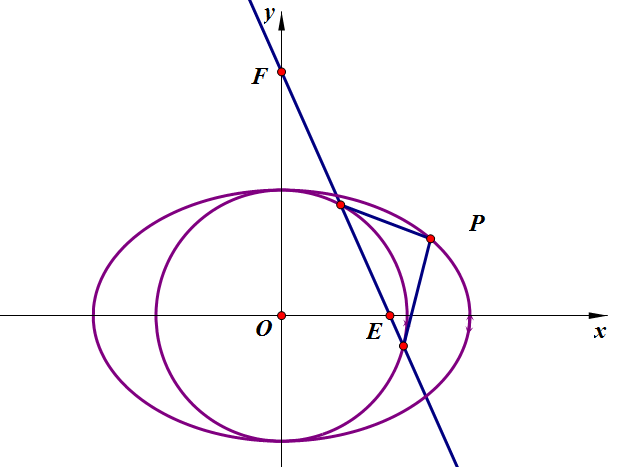
分析：设，则切点弦方程为，

，

所以，

当且仅当时取等号．

例8 直线与抛物线交于两点，为抛物线上的一点，，则点的坐标为 ．

解法一 求交点坐标

联立得，

可解得．

设，由题意，，得.

又，所以，

观察方程的结构特点，可知是方程的一个根，所以

，继续尝试，得出是方程的一个根，即

，

由已知，所以，或，

故，或.

解法二 设而不求

联立得，

则，

进而，

设，由题意，，得.

以下同解法一

解法三

出现四次方程的原因在于因式中包含了C点与A、B重合的情况，所以，避开数量积等于零的条件，改用斜率之积等于-1．

，

，

，

展开，利用根与系数关系，得

．

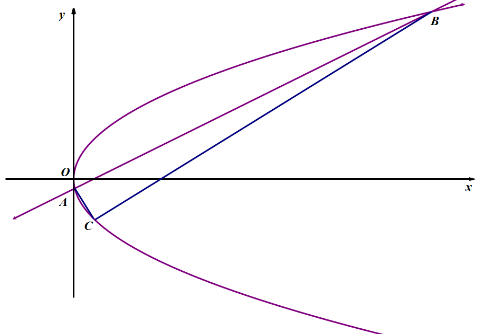
例9（2011全国联赛一11）

作斜率为的直线与椭圆：交于两点（如图所示），且在直线的左上方．

（Ⅰ）证明：△的内切圆的圆心在一条定直线上；

（Ⅱ）若，求△的面积．

思路分析：特殊探路

移动直线使直线与椭圆相交，观察角APB平分线的位置变化，特别是极限位置，当直线与椭圆相切时，求切点的横坐标．

椭圆在第四象限的解析表达式是，

，

令，解得，

猜想内切圆圆心在直线上，

解（1）

设直线:，代入，得

，

设，则，

，

，

所以，角平分线平行于轴，又过P点，

故△的内切圆的圆心一定在直线上．

（2）

所以，

代入，得

，

已知是方程的一个根，所以，另一个根是，

，

同理可得

，

所以．