XYZ分类并非恒久的，不能说一个货物划分为X类，那么这个货物就一直是X类货物。XYZ分类一样也需要滚动的。有些货物的表现特征是反复的，这个月是X类，下个月会变成Y类，再下一个月又变成X类。

另外一个，我们要注意那些连续分类变化，并且呈现出一种趋势发展的货物。

比如图2-15的SKU A和SKU B ，呈现这样的变化趋势，就要值得研究背后原因和快速制定新的对应策略。SKU A 的波动性不断增加，从相对稳定的X类，开始波动，然后变为Z类。至于SKU B则是相反，从很不稳定的Z类，变成了比较稳定的X类。

表2-9 XYZ分类的滚动

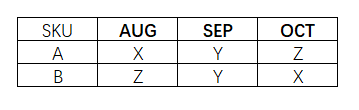
当某些SKU反复地不同的分类里变更，并不能稳定维系在一个类别里，不时是X类，一会又转成Y类，然后又出现在Z类，那么这些究竟应该如何确立它的分类。按照最新的分类是否适合呢？

在这种情况，光是采用最新一期的分类结果，并不足够恰当地确立它的分类。我们可以考虑采用权重，参照一定时期的历史数据从而判断。当然，从数据上来说，越接近现在的数据，越能反映现在的情况，也就说，对于近期的数据可以采取更大的权重，对于远期的数据，采用较小的权重。

这样带来的情况就涉及两个点，一是一定时期的历史数据，这个一定时期是多久？这个并没有铁律，根据行业特征来判断，选择和确立。对于月份的，可以选择近六个月数据；对于周数的，可以选择近十三周的数据；若是使用到年份数据的，那么近三年数据也可以。二是，权重怎么配置？这个也是根据自身判断和选择的，不过权重合计要等于1。近期的权重大，远期的权重小一些。

以下SKU，反复在XY类型中交替，那么可以根据近6个月情况和所占比重，选择定义它为Y类型。

表2-10 XYZ分类的权重分配

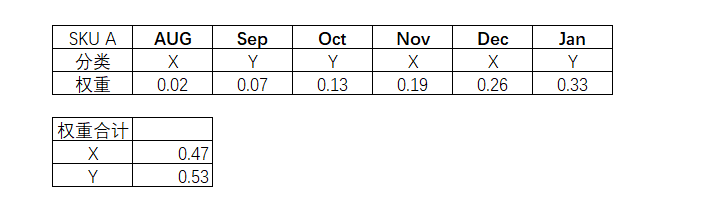
当然，要说直接取最近一期的类型为定义其类型也可以，比如上面数据，可以根据一月份的情况而把它定义为Y类型，不过考虑到有些货物情况的偶发性，建议还是采取一定时期的历史数据作为综合判断和定义。

【小插曲】游程判断Z类货物的随机性

在XYZ分类法中，Z类是比较麻烦的一类货物，它的标准差远远高于平均数，从而表现得起伏很厉害，有时数量很高，有时又很低，甚至更多时候需求表现为0，如果货物价值越高，客户对其需求重视很高，对缺货容许度不大的话，就更添麻烦。

然而，有时管理库存，订货，甚至预测的人，却不会，不能，不敢和相关诸如销售，市场部门探讨，获取他们对此类产品的信息，走向，看法等。那么就数据上，可以运用SPSS软件和结合游程检验方法判断这个货物的销售量的随机程度。如果随机程度不足的话，那么就更要深入研究，了解为什么这个货物用量会起伏。是否数据问题，诸如订单积压，延期等没有及时真实记录需求，或者其他主导原因。

游程检验是对二分类变量的随机检验，主要用于判断数据序列中两类数据发生过程是否随机。

一个仅有0和1两个元素组成的序列中，连续出现0或连续出现1的一组数就称为游程。一个游程中所含0（或1）的个数则是游程长度。

简单的例子，110000100111，这个序列中，就有5个游程，长度分别是2（11），4（0000），1（1），2（00）和3（111）。

如果一个序列具有某种趋势，那么它的游程就会很少，例如

0000101111

又或者如果一个序列具有某种周期性，那么它的游程就会很多，例如

101010101010

任何趋势和周期都不是随机的体现，因此一个随机的序列的游程应该多于趋势序列的游程但少于周期序列的游程。

将一组24期的销售数据输入到SPSS中。

表2-11

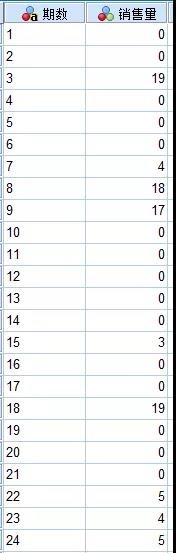
并在菜单栏选择选择分析-非参数检验-旧对话框-游程，然后把销售量作为检验变量列表，平均值为分割点。

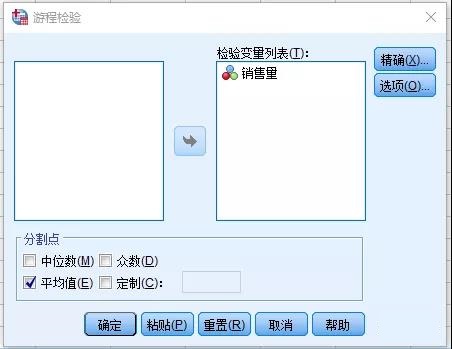
图2-12

在精确选择框中选择仅渐进法。其中仅渐进法默认的显著性水平为0.05，这个就说大于0.05的结算结果则视为随机，否则为非随机。

图2-13

上述三种方法的比较；

仅渐进法：系统默认的计算显著性水平的方法。计算显著性水平时基于检验统计量的渐进分布假设，如果显著性水平为0.05，检验结果被认为存在显著性差异。渐进方法的显著性水平要求数据量足够大，如果数据量比较小或频率过低，即检验结果可能失效。

蒙特卡洛法：即精确显著性水平的无偏差估计。它是利用给定样本集，通过模拟方法重复取样来计算显著性水平，该方法不要求渐进方法中的假设。对于处理不满足渐进假设的巨量数据，同时由于数据的巨量无法得到精确的显著性水平，可以选择该方法。选择该方法时，需要在置信度级别输入计算的显著性水平的置信度，系统默认为99%，在样本数文框中输入取样数量。

精确：指精确计算显著性水平的方法。该方法得到精确的显著性水平，不需要渐进方法的假设，不足之处是计算量和所需内存太大。选择该选项后，可以选择每个检验的时间限制来设置计算时间限制。默认时间限制为5分钟，超过该时间系统会自动停止运算并给出计算结果。

最后通过SPSS运算，我们得到结果如下:

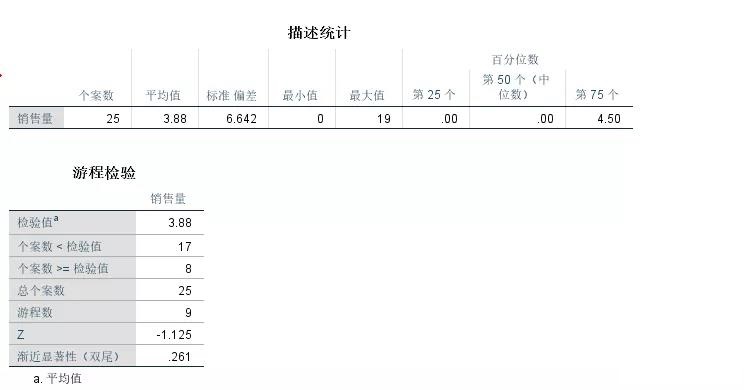
图2-14

在描述统计中我们可以得到相关样本数据的结果，标准差几乎是平均值的2倍，假如定义系数大于1为Z类货物，这个货物是非常波动厉害的Z类货物。

通过游程检验结果得知，少于平均值的样本数为17个，大于或等于则有9个，游程数有9个，其中渐进显著性结果是0.261，大于0.05，也就是接受这些数据是随机的说法。

因此这个销量我们可以认为有很大的随机因素而导致的。

这么一来，我们可以通过诸如使用双堆法，设立每一堆的库存线，而这些数据样本最大值是19，可以考虑用最大值的80%等来设立库存水位线，又或者计算销售获利和残值的临界，来设立库存线等。因为随机是难以把握的未来，并且过去的规律难以对这种随机起着很强的指导或者参照作用。