很多安全库存公式，包括经典的安全库存公式都是基于正态分布的，不过现实并非都必然是正态分布的状态。正态分布是属于连续分布的一种。除了正态分布，往往还有离散分布。

现实生活中，往往容易面对一种情况，就是有些货物尽管备了货物，由于某些特殊情况，库存基本在某段时间（比如上午）基本消耗完毕，在这个时候，是否作出迅速补货的决策是一个挑战。一旦指示加急补货（由于销售比预想要高，突然成为热卖，若作出常规补货，就可能错失这个销售热潮时段），引发的问题就是两个方面考虑，一是是否加急，加急补货多少，二是加急补货发生的费用是否值得。

对于加急补货多少，实际上就是一个库存量建立的问题。不过建立的量应该有多少，则是一个不容易的挑战。因为需求往往具备不确定性，如果库存过少，容易导致需求得不到满足，最终流失客户，损害企业的盈利。如果库存过多，又容易造成过剩而废弃，同时库存积压资金，不流于周转，因此会为企业带来沉重的负担。

尤其在零售业中，消费往往都面临许多不确定性，而对于消费，一旦缺货无法满足顾客即时的消费需求，除了错失盈利机会外，影响消费者的体验感，还有最大的可能性，就是拱手把这个潜在的消费机会让给了竞争对手，从而损失市场份额。

消费是具备很大不确定的随机性，有时可能一件商品也卖不出，有时又可能卖出好几件。像这样的情况下应该怎么制定库存策略呢？

在这个情况，泊松分布有助于我们制定相应的策略。

泊松分布是适合于描述单位时间内随机时间发生的次数的概率。因此，未来一个时间段的销售货物的件数的概率是可以通过泊松分布计算出来的，这是建立库存的一个数据依据。它有助于找到一个时间段内发生若干事件的概率。

其函数分布公式为

泊松分布的概率质量函数给出了在一个时间段内观察到k个事件的概率，该时间段的长度和每次的平均事件。其中e 是固定的常数，为自然对数的底数，是一个无限不循环的小数，一般取值根据自身需要在前几位，e=2.71828…，x是事件出现的次数，K！是K的阶乘，即K*（K-1）*(K-2)…，而则是x的期望值。当时，泊松分布接近于正态分布，而当的时候，可以认为泊松分布呈正态分布了。

泊松分布首先不和正态分布一样，它是应用在离散分布上的，除此之外，还必须适用以下四个条件：

1、这个事件是一个小概率事件。所谓小概率事件是一个事件的发生概率很小，那么它在一次试验中是几乎不可能发生的，但在多次重复试验中是必然发生的。统计学上一般用P值分析。

2、事件的每次发生是独立的，不会互相影响的。A和B的发生是独立的，不是因为A才有B这种关系。

3、概率是稳定的。

4、事件发生的概率与时间段的长度成正比。例如，事件在2小时内发生的可能性应是事件在1小时内发生的可能性的两倍。

因此可以这样理解，比如某个订单处理中心，某个时段如一小时内平均接到录入的订单10张，虽然平均每小时是10张订单，不过理论上在一小时内，他们可以接到任意数量的订单，不管是5张还是20张，而每张订单都是独立的，没有理由一张订单会影响到另一个人下订单，也就是A订单的发生不会B订单发生的概率，并且假设在前半小时收到订单的概率和最后半小时收到的概率是相同的。

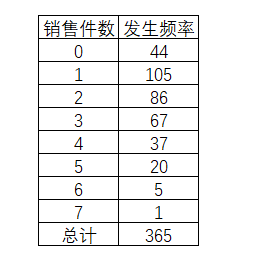
某饮料过去一年的销售数据，其中有44天并没有发生销售，而有105天则每天有1瓶的销售发生。

表3-18

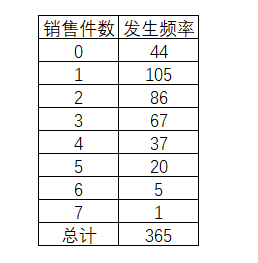
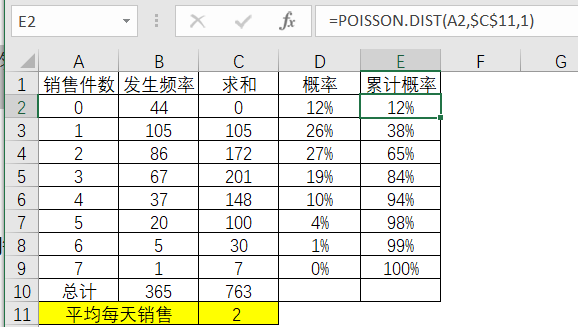
从表3-18这个历史销售数据，即包含了365天的样本数据（运用泊松分布公式的样本数据请尽可能地多）中得知了每日的平均销售量在2瓶。这个情况下我们使用EXCEL的函数公式Possion.dist去计算每日销售件数的概率分别是多少，从而判断建立库存量的水平位置是多少。

如果代入以下泊松分布的公式来计算：，公式中的X就是每日销售件数，也就是变量。值是表示过去的平均销量，也就是每日平均销售2瓶。K是期望的每日销售。可以是1，2，3，即代表每日销售1瓶，2瓶，3瓶的期望。而e则是常值，为2.71828

最方便快捷的，自然适用EXCEL函数。Poisson就是泊松的英文，根据Excel版本的不同，有些需要打上Dist，有些直接Poisson就可以了。而第一位输入数字0就是期望值，第二位输入数字12就是平均值，False是期望值对应的概率，True则是累积概率。

概率分布计算：

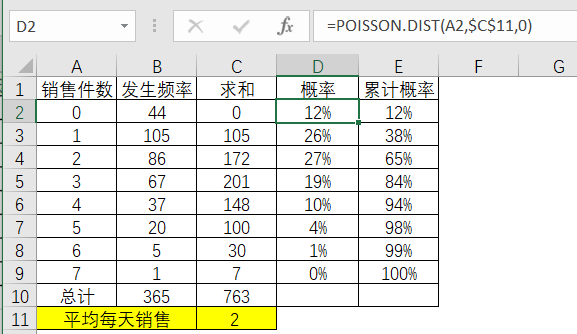
表3-19 Excel的泊松分布概率计算

累计概率分布计算：

表3-20 Excel的泊松分布累计概率计算

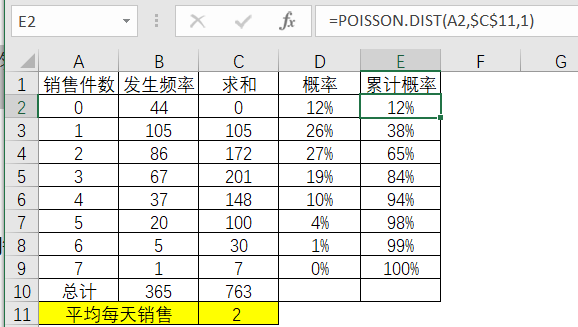
通过计算结果得知，过去每天销售件数的概率和累积概率。也就是说，每天不会有任何销售的概率是12%，而能够卖出2瓶的概率则是27%。从累计概率来看，就可以指定合理的库存数量，当库存建立在6瓶的情况，至少有99%的概率是满足销售需求，只有不到1%的概率会发生缺货的情况。

值得注意的是，概率并非表示一定发生，它是指可能发生或者可能不发生的机会以数字表示，也就是即使90%甚至99%的概率也会发生缺货，即使有26%的概率发生每天卖1件货物，并不是说每个月有26%的日子卖1件货物。

泊松分布是根据过去单位时间内随机事件的平均发生次数，推断未来相同单位时间内随机事件发生子在不同次数的概率，也就是说，通过泊松分布来计算出现的概率，是基于过往历史数据的情况下而得出的，由此建立的库存策略，是相信以往这个规律会重复在未来上，并且未来不会有太大的变化。否则，这个情况下计算的概率，在未来存在不适用性。

假如这个数据是某电商的产品，如果公司通过手段增加流量，又或者通过某些宣传文章导流成功等，从而单日的销售件数会有很大的变化，和既往历史数据存在的规律存在条件不一致，这个概率就会存在变化了。

如果没有什么大的未来事件，销量基本稳定在这个变化之内，那么我们可以选择常规库存计划定在4瓶，因为备件在3瓶，概率相差有10%之大，但是增加到5瓶，概率也只有提升了4%左右。

另外，泊松分布是要独立的条件下使用，如果是某些产业，涉及BOM的（比如A零件是XYZ三个部件组成），那么用泊松分布是计算A和X则是不太符合。

尽管泊松分布的计算，帮我们认识了发生的概率，从而考虑是否指定加急订货而来维持必要的库存，不过对于是否值得进行加急补货这个问题，不妨引入指数分布来思考库存管理的策略。

所谓指数分布，是在概率学和统计学中，用以表示独立发生的随机事件的时间间隔。实际上就是描述泊松分布中时间发生时间间隔的概率分布。因为指数分布必须有如下的适应条件，而这些条件实际上就是泊松分布的前提。

1. x是两个事件发生之间的时间间隔，并且x>0;

2. 事件之间是相互独立的；

3. 事件发生的频率是稳定的；

4. 两个事件不能发生在同一瞬间。

最常见的是一些足球投注网站，可以见到有如下的投注，这个就是涉及指数分布，就是赌在某个时间间隔段发生随机事件（如进球，红牌，点球）的出现与否。比如1-10分钟（即0：00-9：59）出现1个进球的情况等。

图3-18 投注说明，来源于网络

那么在库存策略应用上，就可以运用这个指数分布处理。通过这个分布来计算在某个时间段里，出现某种情况（比如销售需求）的概率。

指数分布的公式如下：

其中λ > 0是分布的一个参数，常被称为率参数（rate parameter）。即每单位时间随机发生该事件的次数。而x则是表示给定的时间长度，u则表示随机事件发生一次的平均等待事件，所以λ可以视为的倒数，那么是常值，是自然对数等于2.71828的基数。

指数分布中的公式表明 λ随机发生的次数越多，那么两个事件之间的时间间隔必然越短。

其累积分布函数公式是如下，而在库存管理上，则主要应用到这一个公式。

回顾过去一年的销售情况，根据刚刚泊松分布的计算，因此今天我们备库存4瓶的饮料。而商店是从早上7点开始营业直到晚上12点，在营业时间过了一半的时候，也就是中午1点的时候，该饮料已经销售了2瓶，那么剩下的2瓶库存很可能在下午时段内销售完毕，尤其附近举行运动会比赛，不管参赛选手或者观众都有机会来到商店购买该饮料。

通过这些数据，我们知道了过去的6个小时内，平均每小时销售2瓶饮料，而且购买这些饮料都是随机事件，相互独立的，并没有因此决定下午一定售卖出这种饮料。那么使用指数分布，可以得出接下来的6个小时是否发生销售，该发生的可能性有多大？

EXCEL的函数expon.dist（根据EXCEL版本可能有所不同）可以有效地快速计算出其累计概率。

表3-21 Excel中指数分布的计算

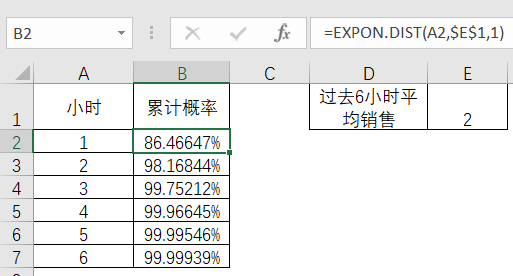
表3-21计算了接下来的6个小时的累计概率，按照前6个小时内平均销售了2瓶的情况来看，接下来的2个小时高达98.16844%会发生销售，甚至到了第6个小时，这样的概率会非常接近100%，也就是具备非常大的可能性会发生销售情况。考虑到营业时间是到晚上12点，而现在才是中午1点，根据指数分布的计算，发生销售的机会很大，同时考虑到时间足够长，那么剩下的2瓶库存就很有可能不足够，加急货物就是值得安排了。

不过，指数分布是具备无记忆性的。所谓的无记忆性是指过去的发生与否并不影响未来，尽管在6个小时内发生销售的概率是99.99939%，但在前三个小时内很可能并不发生，在第4个小时才发生第一次的销售，前三个小时实际只是沉没成本，并不会影响第4个小时的销售。

泊松分布和指数分布计算的概率问题不尽相同，不过两者是可以互相结合的。泊松分布可以帮助计算过去平均一小时有5人购买结账了，接下来一小时有8人进行结账的概率；而指数分布则帮忙计算了过去的20分钟有1个人过来结账，接下来的10分钟有人来结账的概率。

它们的结合，有助于思考和制定库存策略。

【小插曲】如何验证泊松分布

泊松分布和正态分布是属于不同的分布范畴。前者是属于离散分布，后者则是连续分布，不过两者是可以互通的。当泊松公式中的值很大，一般认为是20，就可以视为正态分布。泊松分布的极限就是正态分布。

图3-19显示随着值的增大，分布越发变得接近正态分布。

图3-19 泊松分布向正态分布的趋近，图例来源于网络

有些需求不稳定的情况下，甚至出现连续数期的0需求时，这种不连续的数值分布很容易就被认定是泊松分布，不过事实并非如此。

下图是美国航空公司同一个时间段内发生碰撞和死亡的分布数据，其中第一行的碰撞数据分布是符合泊松分布，而第二行的死亡数据则不符合，虽然两者的数据分布都有出现0数据的情况，但这种数据分布并非理所当然地认为是泊松分布。

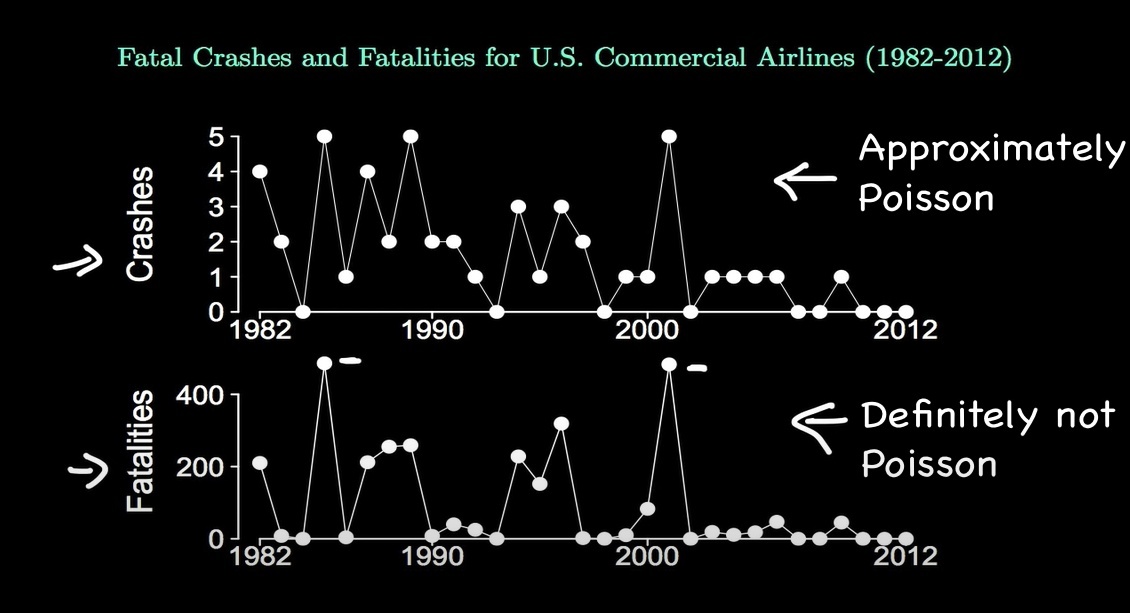
图3-20 美国航空公司事故数据图，来源于网络

某饮料过去一年的销售数据中，有44天没有发生销售情况。这种数据是否属于泊松分布，利用EXCEL进行卡方检验，可以帮助分析验证。

表3-22

假设表3-22的数据是符合泊松分布的。如果求得P值小于等于0.05，就是这个是小概率的事件，我们有理由怀疑它的真实性，从而拒绝这个假设，反之我们则相信这个假设。这个过程就称为卡方检验。

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。

其公式是

为i水平的观察频率，为i水平的理论频率，n为总频率，当观察频率与理论频率一致的时候，=0；观察与理论频率越接近，差别就越小，的值就越小；反之观察与理论频率差别越大，的值则越大 。

首先通过相关计算，从实际观察到的数据计算出概率和累计概率。

表3-23

因为要进行卡方检验，有了观察数据之后，还要引入理论频率这个数据，从而做出比较来验证吻合程度。

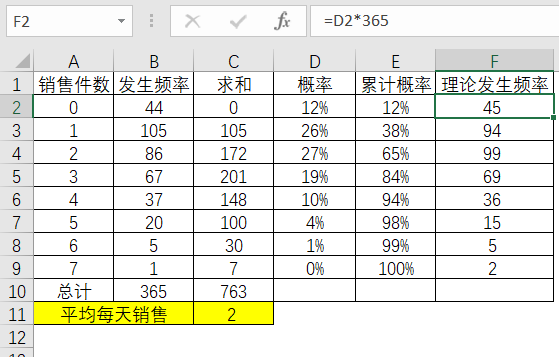
根据每个销售件数的概率乘以365天来计算对应的理论发生概率。

表3-24

利用EXCEL函数chisq.test计算出P值

表3-25 P值计算

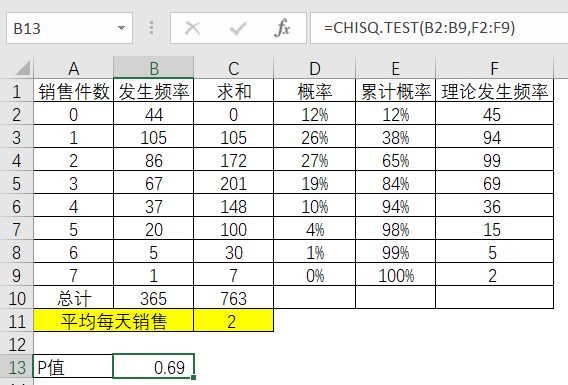
P值大于0.05， 意味着接受假设，即这个分布就是泊松分布。这样一来，我们就可以相信计算的结果，因为符合泊松分布的规律。