英格兰超级足球联赛作为世界上最受欢迎的足球联赛之一，吸引了世界各地的球迷关注。而英超历史上最成功的足球俱乐部——曼联，自然也是世界上最受欢迎的足球俱乐部之一。2015-2016赛季开始，阿迪达斯以7.5亿英镑赞助曼联，成为其全球技术赞助商和品牌版权合约商。在其2020-2021年财务年报中，零售、商品和授权产品收入达9200万英镑。

为了在这个新赞助的项目上，阿迪达斯邀请了新的计划工作人员。在考虑如何制定计划前，他们开始从头回顾情况，进行分析。

阿迪达斯为曼联提供球衣产品，在赛季初会按照计划准备一次性的订单来建立库存和销售计划。而印有明星球员号码和名称的球衣自然是热销对象，当然阿迪达斯在曼联官方门店也会提供印刷服务，只是由于条件制约，成本会稍微高，但满足他们要求，让他们买到喜爱的球衣自然也是曼联俱乐部的工作目标。

除此之外，即使不是大受瞩目的球员也不乏追随者，尤其是自身青训系统出来的球员更受本地球迷热捧，那么阿迪达斯也会考虑利用空白球衣来满足这些可能会大幅提升的需求，一旦在赛季中一些球员表现大为出色，远超预期，球衣的销售自然会远超预期准备，获得球迷追捧。

阿迪达斯以每件球衣24英镑的批发价格卖给曼联，曼联在其官方商店出售的零售价格大概在60英镑左右。而阿迪达斯的成本取决于制造商，送往曼联的一件印有球员名字的球衣和一件空白球衣的平均成本分别是9.5英镑和9英镑。而协助曼联在其商店加工一件空白球衣，在背后印刷号码和名字的成本大概是1.2英镑。

一旦到了赛季后期，球衣容易成为积压库存，伴随着曼联可能签约新的赞助商，球衣款式作出改良等，或者球员有转会安排等，阿迪达斯安排以打折形式卖掉这些球衣。打折后，那些印刷球员名字的球衣平均销售价格是7英镑，而对于空白球衣，购买后，一旦新赛季，或许在款式上更新，不过考虑到有新的球星加盟，即便是旧款球衣，球迷依然乐意印上新球星的号码和名字，因此空白球衣打折的追捧程度也不低，甚至在转会窗口期间，出现销售热潮，因此对于空白球衣的打折，阿迪达斯确立的折后价是8英镑。

计划人员根据各种因素分析，如以往销售，球队和球员表现，市场情报，提前的订单需求，相关的预测，得到如表5-3球衣的预测结果，并且预测结果经过验证，符合正态分布。

表5-3 球衣销售预测

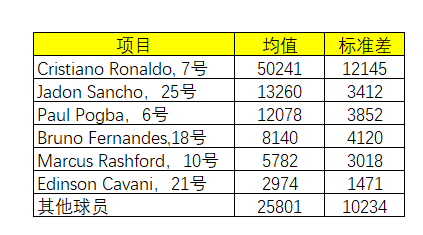
其中作为金球奖得主的葡萄牙球员Ronaldo当然最受欢迎，另外的明星球员也被估计获得大量追捧，他们球衣销量预测数据均超过阿迪达斯与球衣的合同制造商约定的最小批量1500件。虽然其他球员的需求比较难预测，也不可能超过最小批量，因此阿迪达斯采用了累积预测方法，得到其他球员的需求综合超过25000件。

当球队成员开始进行紧张的赛季前备战训练时，阿迪达斯的计划人员也紧张地制定备货及订单计划。

对于这些销售获得利润，而销售情况不理想，则通过打折的方式，这样可以让计划人员想起使用报童模型这种数学模型。

所谓报童模型，是指有这样一位卖报纸的报童，他每天需要根据所预测的明天的销量来决定订货的数量，他必须要在报纸销售这个随机需求发生之前制定订购的决策（订购多少货），这个订货时机仅有一次，并要保证在销售前收到所有的订货。而销售发生后，他才会知道究竟是订货过多还是过少。这种情况下，他每销售一份报纸，获得利润是零售价减去采购价，而销售不出的报纸要赔偿的，就是采购价和退回价的差价。

为了在赛季前为下一期的曼联球衣销售完成备货计划，并安排订单。计划人员把知道的要素整理如下

曼联球衣的官方零售价 ：>= 50英镑

阿迪达斯的球衣销售价格：27 英镑

阿迪达斯的印刷球员名字球衣成本（简称球员球衣）：9.5英镑

阿迪达斯的空白球衣成本（简称空白球衣）：9 英镑

曼联门店印刷的加工成本: 1.2 英镑

打折的阿迪达斯的空白球衣售价：8 英镑

打折的阿迪达斯的印刷球员名字球衣售价：7 英镑

对于订单的要求，如果订货太多，一旦卖不完，从而赔钱；如果订货过少，导致球衣不够销售，就会减少收入。因此，存在一个最优的采购量，使得收入最大。

在计划之前，确立两个成本：

1.超额成本：以符号表示

超额成本是指订货过多产生的订货成本，不过由于正常渠道销售不了，通过打折等方法处理并得出残值。计算为球衣的成本减去对应的打折后售价。可以理解为多销售一个单位的货物而增加的损失，所以，球衣的超额成本是

球员球衣：9.5 – 7 = 2.5 英镑

空白球衣 ：9- 8= 1 英镑

2.短缺成本: 以符号表示

短缺成本就是因为没有足够的货物导致销售不成，而丧失了销售利润的损失，某些情况下还需要增加罚金。计算为销售价格减去成本，可以理解为多订一个单位的货物而增加的利润。所以，球衣的短缺成本是

空白球衣：27- 9- 1.2 = 16.8 英镑

球员球衣：27-9.5 =17.5 英镑

球员球衣的短缺成本先保留，因为一旦球员球衣出现短缺的时候，可以用空白球衣马上安排印刷来补货。

制定备货计划，首先要考虑满足明星球员的球衣量，但是也要考虑一旦这些需求不如预期，最终只能残值处理。对于球员球衣，先行一定量的备货，并以空白球衣作为提高灵活性的考虑显然更为合适。

制定的备货计划，库存既不能过多，以免增加超额成本，又不能过少，以免造成短缺成本，最优的情况就是既没有过多也没有过少，那么就是超额成本刚好等于短缺成本的时候了。

如图5-3。红色线为超额成本，蓝色线为短缺成本，当订货量去到两者交汇点，就是目标了！

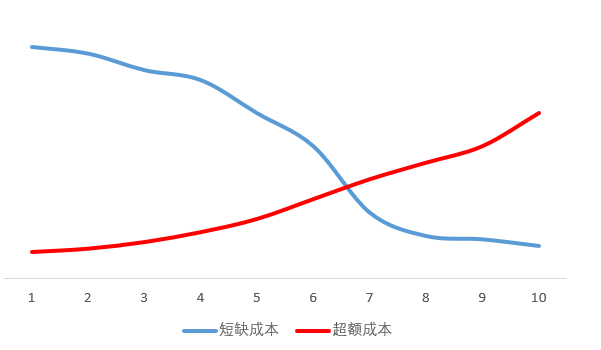
图5-3

超额成本的计算公式就是，而缺货成本的计算公式则是。其中指的是需求的分布函数，即需求量小于或等于Q的概率。一旦等于的时候，即两者取得平衡，既没有超额也没有缺货，得到的结果为

这个就是临界比率（Critical Ratio，简称CR）,比率值为0到1之间的范围，得出的百分比就是指使成本最优化而设定的临界比率

通过这个公式，可以计算空白球衣和球员球衣的临界比率。

空白球衣的CR = 16.8 /(16.8+1) = 0.94 (保留两位小数）

这意味着我们准备空白球衣，94%为准备应付情况，有6%为专门为明星球员备用在上商店印刷的。

不过空白球衣和球员球衣从合同制造商得到的价格是不同，当用空白球衣准备作为球员球衣的备用时，实际上成本是减少了，换言之在这点上，存在了利润空间，即9.5-9=0.5英镑。但是空白球员要额外增加1.2英镑的商店印刷费用，才能转换成其他球员球衣，所以又变成1.2-0.5=0.7英镑，也就是转换过程中实际上增加了0.7英镑的成本。所以球员球衣的短缺成本并非27-9.5 = 17.5英镑。考虑到使用了空白球衣补货，又考虑到认为设定94%的临界比率，也就是6%是发生的情况是空白球衣转换为明星球员球衣，94%的空白球衣就是用用以印刷为其他球员球衣。

那么球员球衣的短缺成本是那么短缺成本就是 6% *（27-9-0.5）+94% * （1.2- 0.5）= 1.71（保留两位小数）

套用临界公式，可以计算球员球衣的临界比率 为 1.71/ （1.71+ 2.5） = 0.41（保留两位小数）

知道这个临界比率后，同时也知道平均值，标准查，这就可以用正态的概率计算公式来计算明星球员的订货数量。利用Excel的NORM.INV计算临界比率下，对应的要达到这个比率的数值。

那么就可以计算在此情况下，各明星球员的球衣订货数量。

表5-4 Excel中订单数量求解

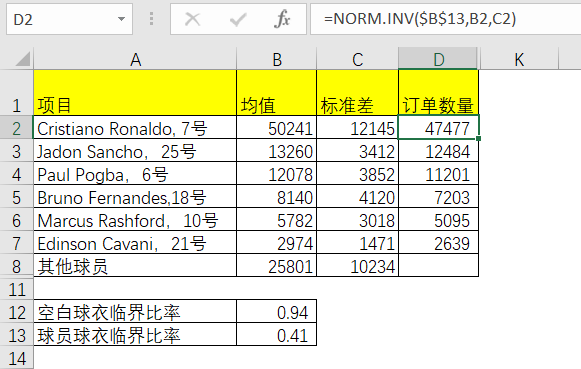
（注：以下临界比率0.94和0.41均只是显示两位小数，并非0.94和0.41这两个精确的数字，因此以此计算的订单数量结果根据Excel自行运算而得）

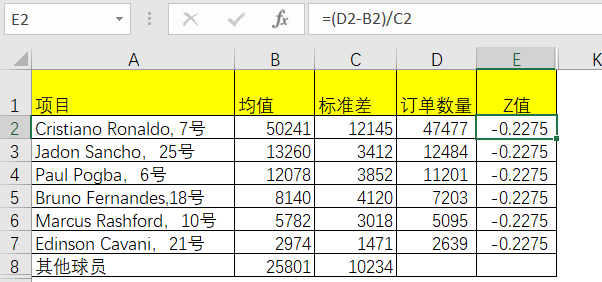
通过我们计算的下订单数据，发现基本上都达不到平均数，也意味我们的订单数可能不满足需求，那么这个不满足实际上可以通过熟知的Z值公式求出。

首先求Z值，公式如下，

其中Q是下订单的数量，μ是平均值，σ是标准差。例如 Edinson Cavani，21号，其Z值为 （2639- 2974）/ 1471 = -0.2275。

表5-5 Excel中Z值的求解

得知对应的Z值之后，便可以利用预期短缺的计算公式来算出预期短缺的数量：

该公式是基于需求服从正态分布，其中Q就是订单数量，μ是需求的均值，σ是需求的标准差。订购了数量为Q的时候，而企业的库存是超额还是短缺，取决于需求，当需求大于Q的时候，才会出现预期短缺。反之就会出现预期超额。而本次订单数量少于均值，因此出现预期短期。虽然期望值（预期）和平均值不是一样的概念，但是数学公式计算出来的值是一样的，从概念上来看，二者是完全不同的东西，但是在某些时候二者表达的内涵可以认为等价。

借助Excel函数公式可以轻易地帮助计算。

表5-6 Excel中预期短缺求解

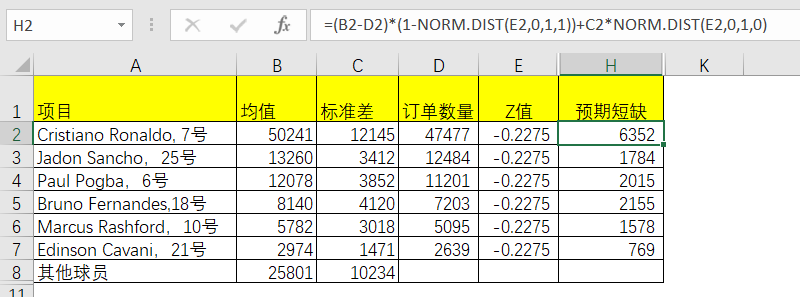
如此类推求得其他明星球员的没满足数量，我们也因此计算出预期售出和预期没售出的。

预期售出= 均值- 预期短缺

预期没售出 = 订单数量 – 预期售出

表5-7 Excel中预期售出和预期没售出求解

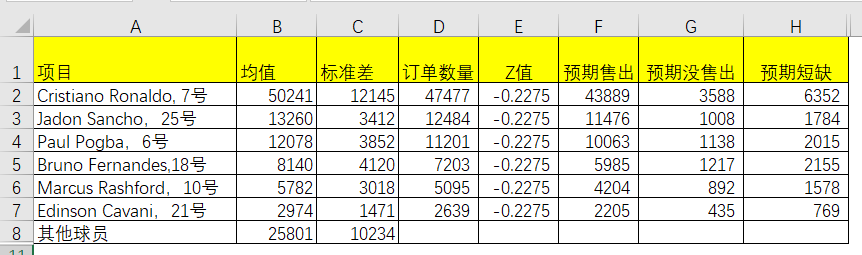
这样下一个目标就是放在空白球衣的。一样用正态的概率公式来计算。但是我们得首先知道空白球衣的均值和标准差。

空白球衣的均值，就是其他球员的均值和明星球员的短缺数量之和（因保留空白以增加灵活性），这个结果为40454件。

表5-8 Excel中空白球衣均值的求解

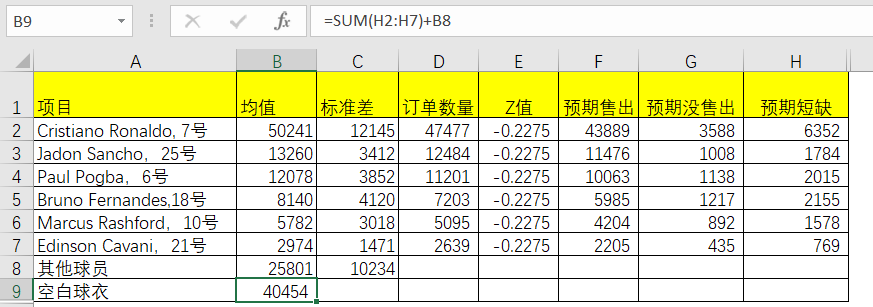
对于空白球衣的标准差，实际上它要包含了两部分，一部分就是明星球员的，一部分就是其他球衣的。方差的开方就是标准差，因此可以利用计算总体的方差进而得出空白球衣的标准差。

明星球员没满足部分不直接用没满足数字来平方，而是引入变异系数（标准差/平均值，简称CV），因为没满足部分是这对球员球衣的，我们要的是空白球衣部分，因此变异系数作为离散的证明，用以概率计算空白球衣的数量。

首先要得出的各明星球员的变异系数。

表5-9 Excel中变异系数求解

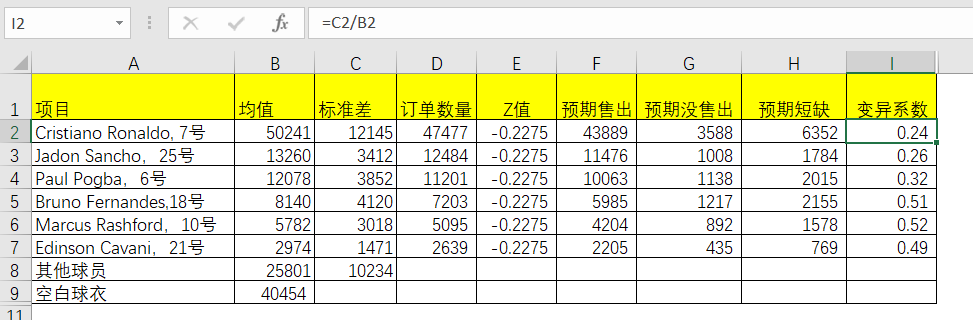
通过变异系数计算出预期短期的标准差，进而求出方差。

表5-10 Excel中预期短缺的方差求解

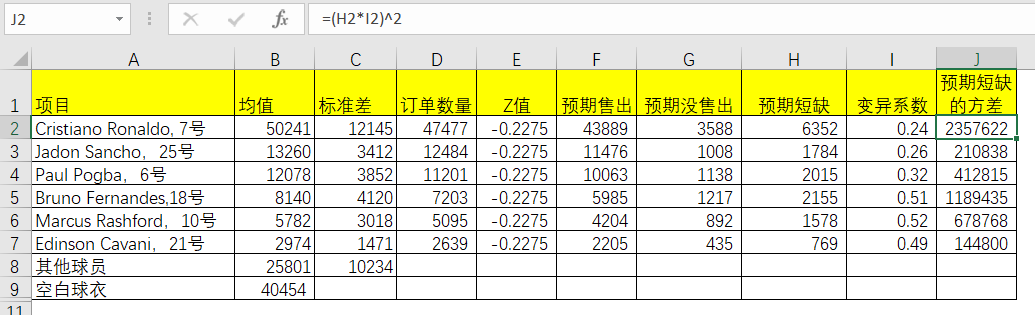
那么就求出空白球衣的标准差了。就是所有销售球衣的方差的开方。

表5-11 Excel中空白球衣的标准差求解

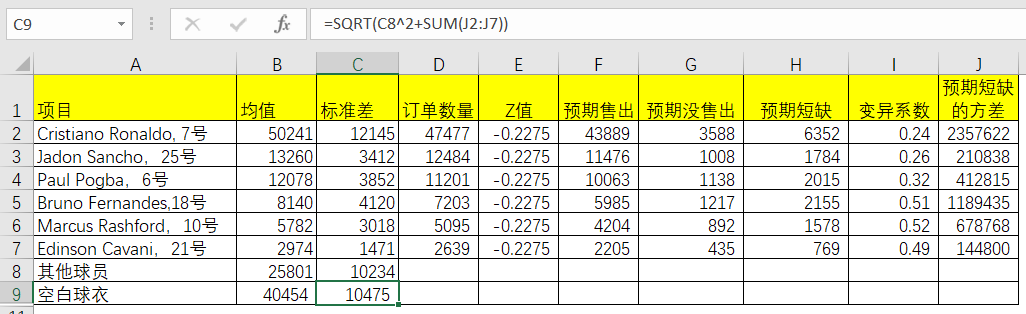
通过计算我们可以得出总体空白球衣的标准差为10475件。接着再用之前的正态方法求出总体空白球衣的订单数，为56741件。

表5-12 Excel中总体空白球衣的订单数求解

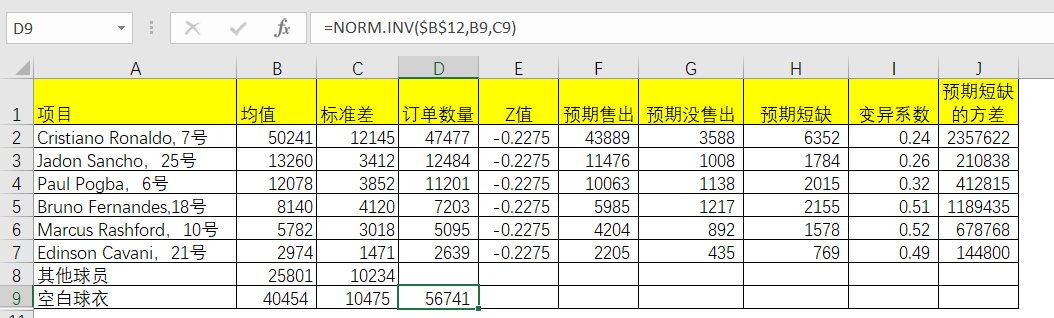
那么所有订单数量加总之后，本次要准备下达订单为142841件。

表5-13 Excel中合计数量的订单数求解

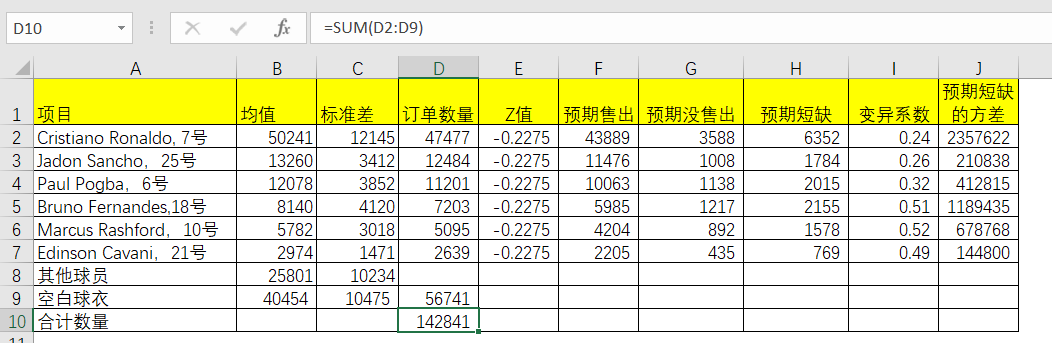
根据订单数量和预期的情况，那么就可以计算出预期的利润。

对于印刷了名字的明星球员和空白球衣，其中空白球衣只会印刷上球员号码等才打折出售，不会将空白球衣直接打折。其预期利润为

球员球衣预期利润=（球衣销售价格-球员球衣成本）x 预期售出数量+（打折球员球衣价格-球员球衣成本）x 预期没售出数量

空白球衣预期利润=（球衣销售价格-空白球衣成本）x 预期售出数量+（打折球员球衣价格-空白球衣成本-印刷加工成本）x 预期没售出数量

这么就可以得出各球衣预期利润和总的预期利润了。总计预期利润为1897836英镑。

表5-14 Excel中明星球员球衣的利润求解

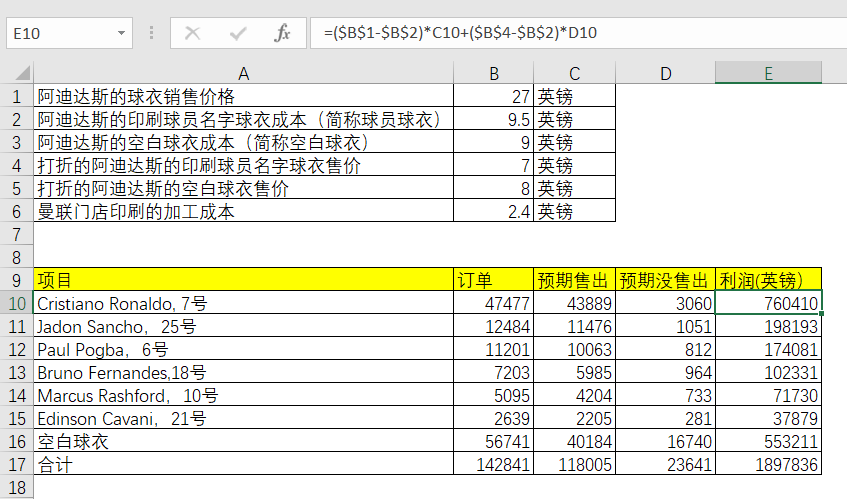
表5-15 Excel中空白球衣的利润求解

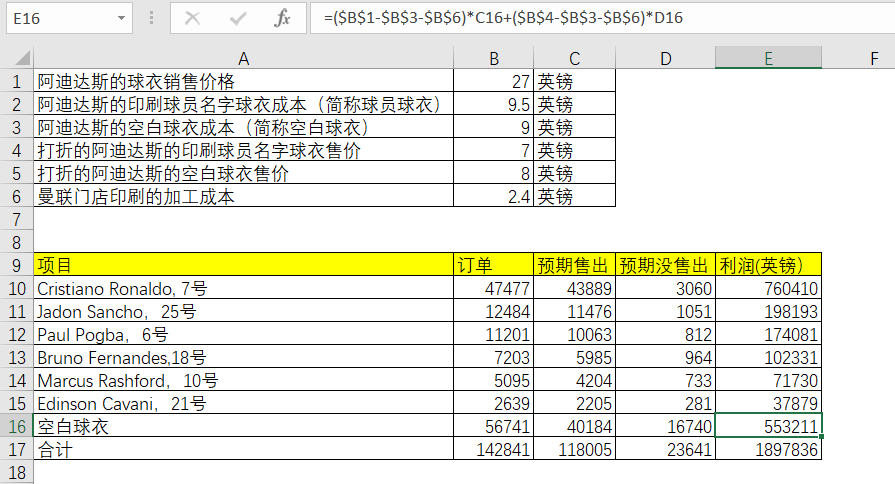
这种报童模式的方法，是基于订单处理的灵活性，再考虑残值，利润和成本后，综合计算的订单数量，也就是基于超额成本和短缺成本处于平衡点的计算。在实际上，当然还有更多的影响参数，比如供应商交货能力，比如品牌圈粉等。因此还要根据实际情况再进行调整。

报童模式中的临界比率，是一个相当关键的指标。它对需求和订货存在一个指示作用，如果需求超过订货数量，就会产生短缺，从而有销售损失，但是如果需求少于订货，就会造成产品过多，带来多余成本。临界比率的应用在于逐利的最大化，确立一个指标，使得既不会短缺也不会产生超额。

临界比率引用广泛，在单周期销售模式的快消品牌中，不少是采用这个模式。某欧洲品牌的销售策略是不断推出新产品，保持顾客对其新鲜感，因此投出一个型号销售后，确立一个销售周期，在周期完结后，大部分情况下都不不会对其补货。

该公司计划下个月投入新型号181159_ECL，在市场中进行销售。它是属于BCD系列的一个单品，而BCD系列在过去的销售业绩统计如下：

表5-16 BCD系列的历史数据

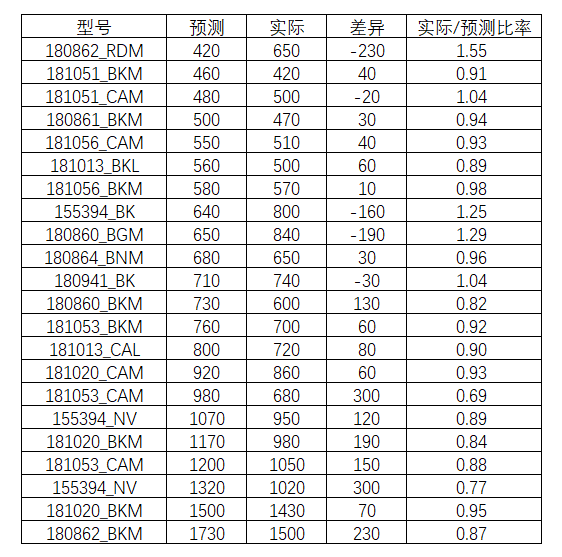
先按照预测数量的多少排序，根据实际业绩和预测进行对比差异，并且计算实际和预测的比率。然后计算这个系列的实际和预测比率的平均值和标准差。

表5-17 BCD系列的平均值和标准差

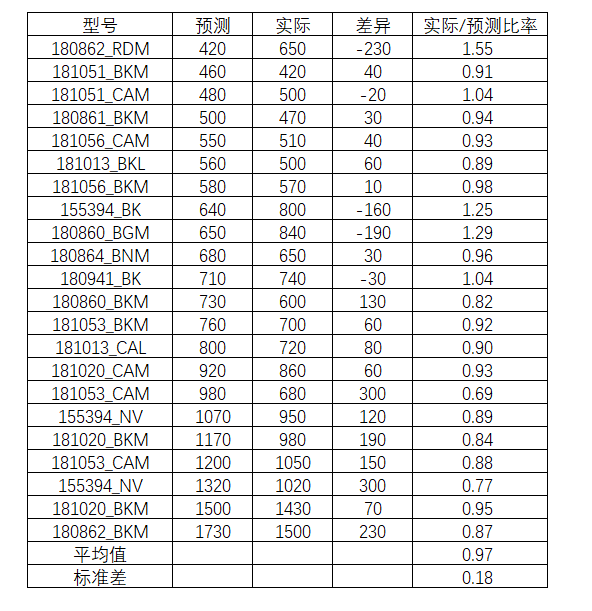
这里主张用整个系列的数据，是因为这些基于过去实际历史数据。预测是以过去的数据为出发点的，而总体预测总比单位预测更准确，因此采用总体数据作为预测的基准。还有就是因为是推出新的产品，新产品可以通过查看可比较的产品来作为判断依据。

现在市场部门预测这个新型号的市场需求在1200，单位成本是30元，售价是80元，如果销售周期内没法完成所有数量的销售，其处理后的残值为10元。

预期实际需求平均值 = 1200 * 0.97 = 1159

预期实际需求标准差 = 1200 * 0.18 = 218

另外，根据销售成本，售价，残值等，得出短缺成本和超额成本。

根据公式，计算出临界比率：

当订货数量定在0.71这个临界比率，有助于取得利润最大化。当然，接下来用Excel的函数公式，就能简单地帮助计算出，在这个临界比率下订购的数量是1280个单位了。

图5-4 Excel中订单数量的求解

除此之外，利用临界比率，结合边际收益和边际成本，可以帮助确立库存建立的数量。该公司的主要热销产品180861_BKM，长期受到客户的追捧。根据过去的历史销售数据记录，得知这个产品的每日平均销售是12个单位。经过验证，符合使用泊松分布的计算条件，从而计算出每日需求从0个单位到24个单位的概率和累积概率。此外，引入一个新的计算依据，即累积以外的概率，比如需求为1的累积概率是0.008%，那么需求在0和1意外的需求就是需求2，3，4……它们合共得出的累积概率就是累积以外的概率。

表5-18

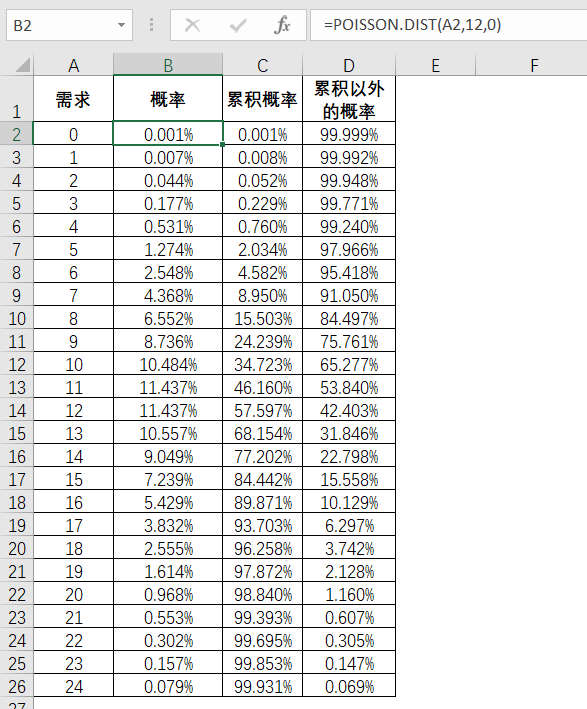
在这么多的需求可能性和响应的概率之下，设立一个预期的库存水平。如果高于这个库存线的需求，视为预期边际收益，而低于这个需求视为预期边际成本。所谓边际收益就是加一单位产品的销售所增加的收益，而边际成本则是每增加一单位产量所增加的成本。

这个预期的库存线的概率，符号表示为F(Q)，其预期边际收益和边际成本分别为

其中

最后合并演化成公式实际也就是临界比率的计算公式

180861_BKM单位成本是30元，售价是80元，如果销售周期内没法完成所有数量的销售，其处理后的残值为10元。计算出CR= 0.71。

通过计算的需求概率，对比之下，最接近临界比率71%的概率是13个单位，累积概率在68.154%，因此我们为了达到利润最大化，也就是预期边际成本等于预期收益，因此库存建立在13个单位。

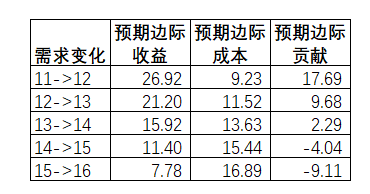
另外，通过下面不同需求的变化进行了解边际收益和边际成本。当预期边际成本等于预期边际收益时，此时边际贡献为0，则利润最大化，而边际贡献从正值转向负值，是14个单位转向15个单位的需求变化时。

表5-19预期边际贡献

计算公式为

11->12 的预期边际收益 = (80-30) * 53. 84% = 26.92 元

11->12 的预期边际成本=（30-20）*46.16%=9.23元

11->12 的预期边际贡献= 26.92-9.23 =17.69 元

如此类推，从而计算出不同的需求变化时，预期边际收益，预期边际成本和预期边际贡献各是多少。因此13个单位向14个单位需求变化时，预期边际贡献最接近0，基于这点考虑，180861_BKM的库存建立在13个单位上。

尽管从泊松分布来看，建立13个单位库存，累积概率只有68.154%，意味着缺货的可能性比较大，不过从成本考虑，为了达到最优成本化，因此即使具备比较大的缺货概率，该公司依然从把库存线建立在13个单位上。