王小明从传统行业转战电商行业，发现备货变成了一个极具挑战性的问题。和过往的经历完全不同。以前在实体店时，当和客人面对面接触，或者凭着客人进店的观测情况，有经验的店员很容易判断出这个客户购物的意愿，对货物的喜爱程度，这些都能转化为有效的参考信息用作备货提示。但是在电商上，都转化为冷冰冰的数字，只有访问率，例如PV, UV或者收藏率，当然对所有经营者都很重要的就是转化率。

小明很快就得知转化率是怎么一回事了。转化率通常是指到达网站后，进而有成交记录的用户比率。

部门内的同事，很多时候做库存计划，往往都参照了转化率得出的购物数量，来预测未来需求和设立库存，当然有些有经验的同事也会借助收藏率，认为收藏率高的产品，很有可能会达成交易，从而设立高的库存以备消费者购买。但是，王小明考虑到，收藏肯定不一定意味着购买，可能仅仅代表访问者有兴趣，有意欲而已。从电商运营者角度，他们可能会考虑各种因素，例如页面吸引力，价格吸引力等等，提升转化率。不过王小明从供应链角度来看，觉得要好好利用一下收藏率，来辨别这些人是否会最终成为购买者，当然前提是运营没做任何改变条件的前提下。

这个时候，王小明觉得可以让贝叶斯推理登场了。

他清楚地知道，贝叶斯定理是描述在已知一些条件下，某事件的发生概率。而贝叶斯推理将后验概率（考虑相关证据或数据后，某一事件的条件概率）作为先验概率（考虑相关证据或数据前，某一事件不确定性的概率）和似然函数（由观测数据的统计模型（概率模型）推导而得）这两个前因导出的结果。

当然贝叶斯推理的公式，他自然也是熟知。

其中，

1) 符号“Ⅰ”表示将某事件成立作为条件，因此 表示假定E成立的H。

2) H表示假说，其概率可能会受实验数据（以下会称为证据）影响。一般来说会有许多互相矛盾的假说，任务是要确认哪一个假说可能性最高。

3) E表示证据。证据对应新的数据，也就是还没用来计算先验概率的数据。

4) 是先验概率，是观察到数据 E（目前证据）之前，假说H的概率。

5) 表示后验概率，是在给定证据E之后，假说H的概率。它就是在有目前证据时，假说H的概率。

6) 是假定H成立时，观察到E的概率。在H不变时，这是E的函数，也是似然函数，指出在给定假设下假说和证据的相容程度。似然函数是证据E的函数，而后验概率是假说H的函数。

7) 有时会称为边缘似然率。此系数对所有可能的假说都是定值，因此在判断不同假说的相对概率时，不会用到这个系数中。

针对不同的H数值，只有 和 （都在分子）会影响 的数值。假说的后验概率和其先验概率（固有似然率）和新产生的似然率（假说和新得到证据的相容性）乘积成正比。

当同事看到王小明使用贝叶斯推理研究计算的时候，他便详细地同事们进行了以上解释。

王小明查看了一下负责的其中一个SKU的转化率数据。这个命名为GT-12的产品转化率是5%。这意味着点进进入该公司自营购物网站访问的客人，查看这个SKU，每100人有5人是最终达成交易购买这个SKU的。剩下的95%可以视为来逛逛，或许有意愿，但最终都是没有购买行为的。

为了更加清晰和避免计算错误，小明绘图做出划分，A表示是最终购买，即转化率是5%的那些人，B就是剩下的，即没有产生购买行为的人。而访问网站浏览这个SKU页面，就存在这两个可能性，一是可能购买，一是可能不购买。将两者之和设定为1，即100%，这被称为标准化条件。这些不同条件划分出不同的可能性。

图5-5

小明通过IT部门的帮助，对有收藏行为的访问者进行分析，他们当中有收藏了再进行购物，有的只是仅仅收藏，最终没有产生购物行为。同时小明知道，还有可能的情况，就是消费者没有收藏，直接购物或者没有收藏也不购物的。

最终他整理了数据，得出了统计数据。有收藏该SKU而最终进行购买的占了70%，没有收藏但是也购买的占了30%；有收藏该SKU不过最终没有发生购买行为的占了20%，没有收藏也没有发生购买行为的则占了80%。

为此王小明又对他的图5-21作出了修改，变为图5-22。

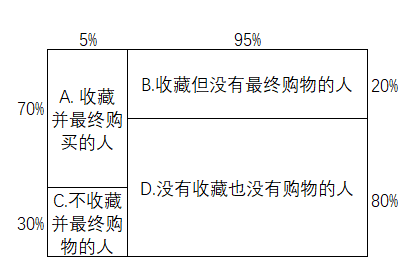
图5-6

左边的70%和30%的表示收藏与否的最终发生购物行为比例，而右边的20%和80%就是收藏与否都没有发生购物行为的比例。小明很快就可以计算出A，B，C，D四种行为的不同概率：

A的概率是 70% x 5%= 3.5%

B的概率是 30% x 5%= 1.5%

C的概率是 95% x 20%=19%

D的概率是 80% x 95%=76%

这四个概率相加恰恰就是100%。

小明根据这个来做库存计划。对于没有收藏的，仅仅是访问的那些客户，做库存计划并不容易。当然可以使用其他方法做预测并以此做计划。但是对于有收藏行为的，某种程度上确认性是增加了一点，并因此提示这个收藏者非常有可能产生购买行为。

小明先把没有收藏行为的排除出去。剩下的就变成新的图示5-23。具备收藏行为的，就剩下两个可能性，最终购物或者最终不购物的。

图5-7

这就是通过一个条件概率，形成了推测过程中的概率变化。那么这两个概率就很容易了。具备收藏的概率为A和C的概率之和，即22.5%。那么A的概率就是7/45，B就是38/45。

这数据明确告诉小明，当访问网站时，客户购物的概率是5%，但是收藏了后，购物的概率提升为16%。这个概率就可以在库存计划的时候，用以参考。比如有500个收藏，那么就相当于有可能产生75个购物行为，以此为基准，结合其他因素小明就可以很好地做一个备货计划。

看到这个备货思路，小明同事们大加赞赏，并希望学习并加以使用。为此小明特意用公式再次进行解释说明。

原有的贝叶斯推理公式是，不过小明代入相关说明文字和数据，使得在场同事一下子明白当中道理。

小明把公式写成如下，并列出运算过程：

王小明从传统行业转战电商行业，发现电子商务充斥着大量数据，通过这些数据进行分析，有助于准确备货。而贝叶斯推理就是他所用的方法之一，从访问量，转化率等，都能进行相关推断，让运营变得更加有效。