报童模式是通过计算临界比率，让超额成本和短缺成本达到一个平衡，从而以此设立销售目标。

所谓报童模式，是指有这样一位卖报纸的报童，他每天需要根据所预测的明天的销量来决定订货的数量，他必须要在报纸销售这个随机需求发生之前作出订购的决策（订购多少货），这个订货时机仅有一次，并要保证在销售季节前收到所有的订货。而销售发生后，他才会知道究竟是订货过多还是过少。

很多时候对于订货，如果购进太多，就会卖不完，从而赔钱；如果购进过少，导致不够销售，就会减少收入。因此，存在一个最优的购进量，使得收入最大。为此制定的备货计划，库存既不能过多，以免增加超额成本，又不能过少，以免造成短缺成本，最优的情况就是既没有过多也没有过少，那么就是超额成本刚好等于短缺成本的时候了。

万家超市从达尔孚巧克力公司采购NN巧克力豆，通过POS机得到的历史销售数据，平均每天销售在50包，标准差是10包。数据表现符合正态分布。

万家超市通过相关分析，得出临界比率是0.625，为了达到成本最优化，制定一个订购量为53包的采购方案。

在每天补货一次的情况，按照此采购方案继续它的销售策略。经过一段时间周，万家超市通过历史记录，发现45%的时间巧克力都能卖完，也就是说，55%的时间里没能卖完。这个时候尽管从成本上考虑，临界得出的数量是优化的，既然45%的时间里发生可以卖完53包，万家超市因此疑惑，那么是否加大备货量，从而增加这45%的概率下的销售额呢？

万家超市的管理层想到了使用删失分布来进行分析。

一个称重磅如果最大承受的重量是150公斤，假如一件170公斤的货物摆上去，数值是无法显示出170公斤，因为极限在150公斤，而观测者最多知道这件货物至少150公斤而已。这种被截断了的数据称为删失数值（Censored Date），而删失就是值的测量或观测只有部分数据的一种条件。

万家超市在这45%的售罄天数里，只能知道可以卖出至少53包，因为只备货了53包，是否可以卖出55，58，乃至60件，它们希望可以通过删失分布（Censored Distribution）来试算。通过巧克力的平均销量，全部售出天数的百分比，每日最大供应量这些信息，就有可能估算出分布的平均值和标准差。

删失分布的计算需要引入两个公式：

各符合意义如下：

X: 平均销量

Q：每日供应量

Fs(Z)：均值以上Z个标准差所处的累积标准差分布

fs(Z)：均值以上Z个标准差所处的标准正态分布密度函数

U：未经删失的需求分布的均值

∂：未经删失的需求分布的标准差

首先有45%的天数卖完巧克力，换言之就是55%没有卖完，这个没有卖完的概率是累积分布。那么计算这个55%对应的Z值，Excel函数能够轻松计算出来为0.126（结果保留三位小数）。

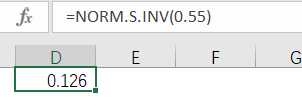
所以公式1 引入数据后，其中53件就是我们通过临界比率计算的每日最大（优化）的供应量，得出。

公式2有点复杂，公式中的X值是被理解为分布上的均值，采用的是正态计算的平均值。通过这个平均值推算出未经删失的需求分布的均值和标准差，因此尽管正态计算的平均值和分布下的平均值有一定的差异，但还是接受这一差异带来的结果，而这个结果是估算。

万家超市的管理人员第二步工作就是计算没卖出的概率下的密度函数fs(Z)，也一样通过excel计算,其中0.126这个Z值已经在公式1计算出来了。最终得到的结果是0.396。

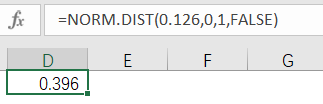
代入数据后得出：

通过简化后，万家超市的管理人员就非常清晰了当中数值所含的意义了。

50是分布下的均值；

53 X 0.45就是卖完的概率45%分布下的累积，即45%的概率下卖完53件;

0.55 X U 就是没有卖完的概率55%下的均值，就是55%没有卖完下的平均值

-∂ X 0.396 就是没有卖完的概率下的密度函数的标准差值。为了让前来了解情况的万家超市的总经理便于理解，管理人员举了简单的例子：一个班身高是160+/- 10厘米，标准差下限可以理解为160-10=150。对于公式为什么采用下限，而非上限，即使用0.55 X U -∂ X 0.396，管理人员进一步解释说如果上加标准差，是很有可能突破已知供应的极限，从而使公式两边不等。

接着对两个公式进行合并计算：

管理人员结果计算，取整数得出 U是52包， ∂是6包，也就是分布下的平均值和标准差是52和6，有了这个数据加上之前计算的临界比率（即最优服务数据）0.625，通过EXCEL计算，在新的估算分布的数据下，取整数结果是54包。

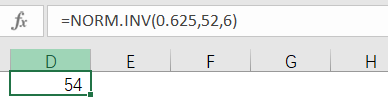
因此万家超市根据这种情况，在超额成本和短缺成本还是不变的条件下，管理人员考虑采购量不止53包，而是改为订购54包了。不过总经理还是另有要求，对相关管理人员设立KPI，要求库存充足率在90%以上，为此管理人员还要进行新的计算，得出每天备货量至少要60包，因此采购量也变更为至少60包。

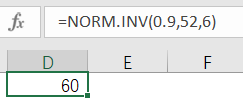
删失分布有助于管理人员在已知极限的需求情况下，如果要突破极限，可以估算出突破多少，从而作出新的决策。当然在新的决策之前，必须确立未经删失的需求分布的均值和标准差。