购物车
购物车
不详
在单指数平滑法中，使用了α这个平滑参数，值在0和1之间，它决定了预测值权重下降的速度，平滑参数越小，结果越平稳，反之则越激烈。不过，它仅仅只是水平的变化。但历史数据并出现趋势变化的特征，就需要增加一个新的参数β，其值也是0和1之间，以应对趋势这个因素。它是单指数平滑法的扩展，称为双指数平滑法，用于预测具有趋势的数据。这个方法是Holt于1957年提出，因此也叫Holt线性趋势法。
双指数平滑法的公式是
n是期数
计算需要上一期的水平值和趋势值为起始依据。双指数平滑法也叫Holt线性趋势法，是因为其数据特征呈现线性趋势，那么最简便的方法就是通过Excel算出线性方程，从而确立初始水平值和初始趋势值。
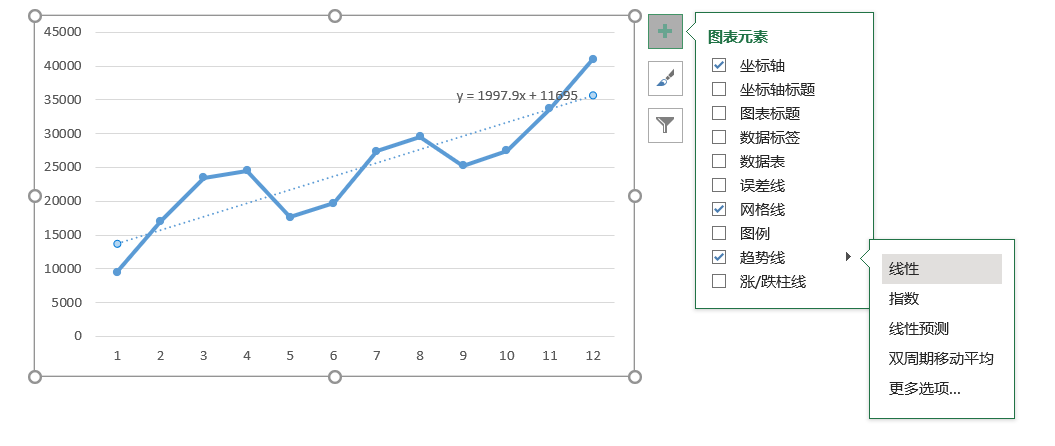
图4-16 线性趋势示意图
这样可以在图4-16中轻易得出线性方程，其方程式Y=1997.9X+11695，其中1998（四舍五入）作为初始水平值，11695则为初始趋势值。
表4-13
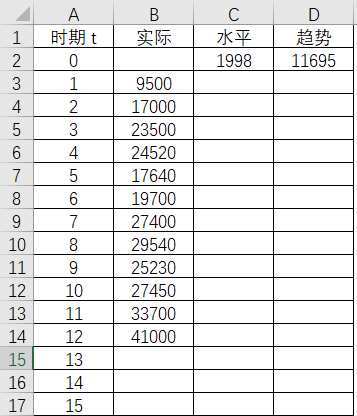
另外也可以选择Excel中的数据-数据分析-回归，得出相关的数值。
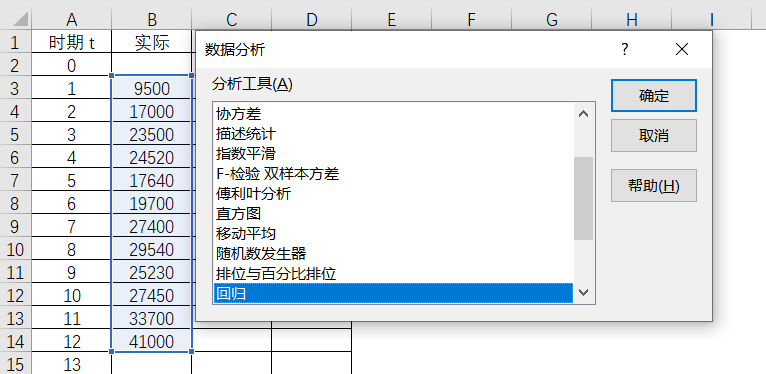
图4-17
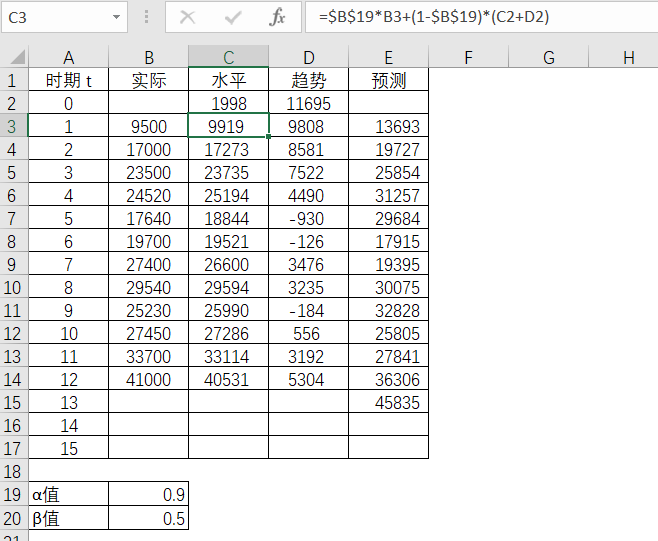
有了初始的水平值和趋势值之后，确立相关的参数α和β的值，就可以代入公式去计算。其中α值为0.9，β值为0.5，就可以得出如下：
这样就得出了第1期的水平值为9919，趋势值为9808，预测值为13693，并如此类推，可以得到后续各期的水平值，趋势值和预测值。
在Excel处求得第1期的水平值。
表4-14 Excel中水平值的求解
在Excel处求得第1期的趋势值。
表4-15 Excel中趋势值的求解
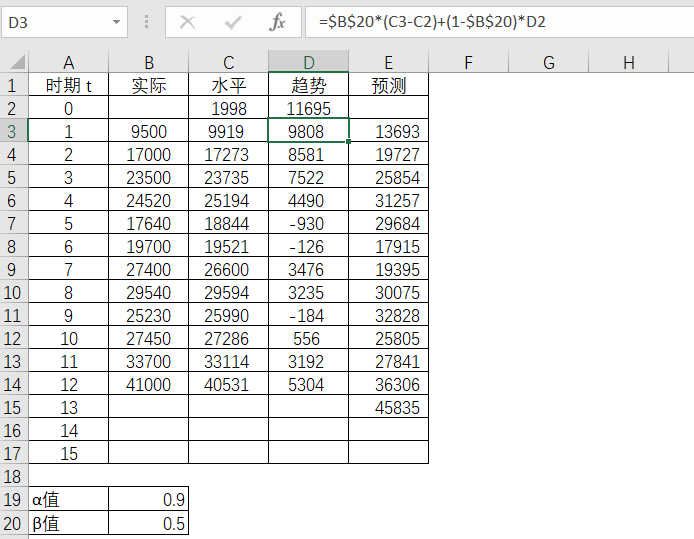
在Excel处求得第1期的预测值。
表4-16 Excel中预测值的求解
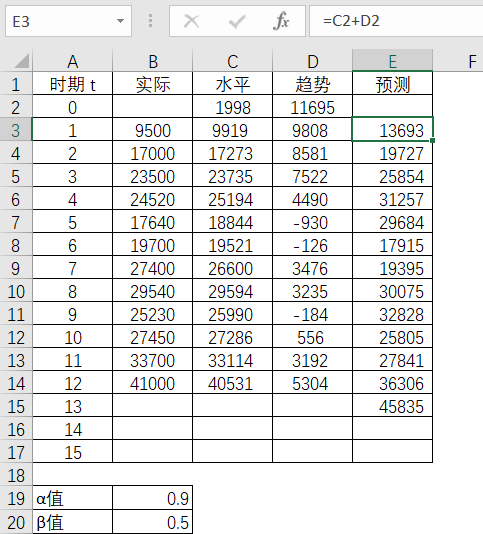
相应的图示如图4-18：
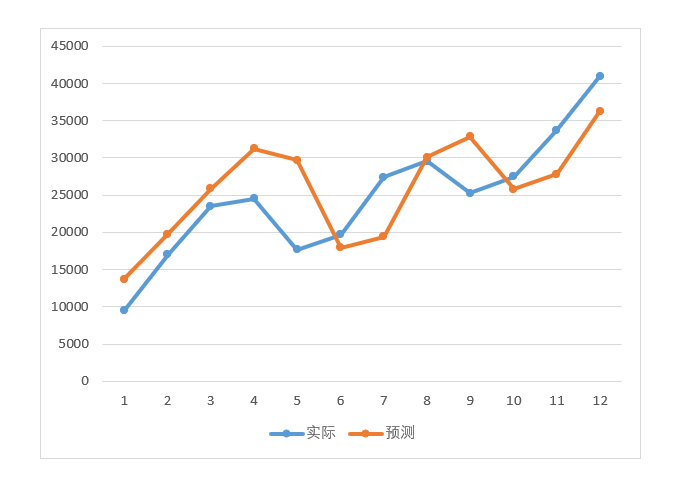
图4-18
在知道第12期的水平值，趋势值的情况下，也可以通过公式求得第15期的预测值。
15-12是指第15期和第12期相差了3期，因此在第12期的水平值基础上，加上3期的趋势值推移，得出第15期的预测值。
3.三指数平滑法：针对水平、趋势和季节性因素
历史数据里除了水平，趋势因素，往往还含有季节性因素。双指数平滑法考虑了水平和趋势因素，使用了α和β两个参数来对应，对于季节性因素，就需要引入多一个参数γ来应对，从而变为三指数平滑法了。
三指数平滑法分为乘法模式和加法模式。其区别是季节性随着时间变化而变化，使用乘法模式；当季节性在时间变化的同时而并不变化，则使用加法模式。
乘法模式公式
n是期数
γ 是季节平滑常数，取值在0和1之间，读作Gamma
2018年第1季度开始，到2020年第4季度，共有16期的历史数据。使用三指数平滑法，同样离不开初始值的确立，这个可以称为观测值，然后通过观测值得出的因素数值，并引用在其他周期上，这些称为实验值，最后就是希望得到预测结果的预测值。因此2018年4个季度的数值可以视为观测值，2019年第1季度到2020年第4季度的数值则为实验值，最后就是预测，如果要预测2022年全年4个季度，那么这4个季度的数值就是预测值了。
表4-17
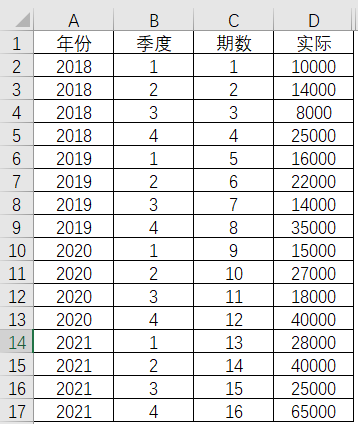
第一步，确立观测值中的季节性因子。通过每一个季度和2018年全年平均值比较，得出各个季度的季节性因子。2018年第1季度的季节新因子就是
表4-18 Excel中季节性指数的求解
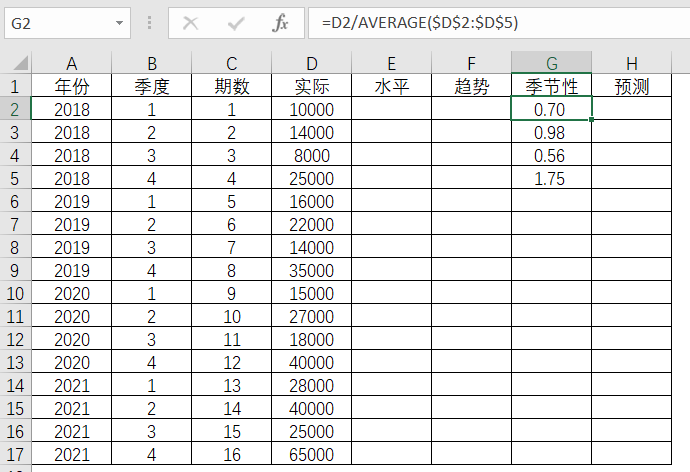
如此类推，得出2018年第1季度到第4季度的各季度季节性因子。由于2018年的全年数据作为观测值，那么水平值和趋势值初始值就是2018年的第4季度了。趋势值初始值为1875，而水平值可以根据当期的实际值，剔除季节性因素而得出，所以初始水平值就是当期实际值除以当期的季节性因子。2018年第4季度的季节性因子在之前计算得出为1.75，那么2018年第4季度的水平值就是
而趋势值可以由2019年的全年平均值和2018年的全年平均值的相比，再除以4个季度得出一个季度的值，就是视为2018年向2019年的趋势，并视为初始值。因此2018年第4季度的趋势值就是
得出了2018年第4季度的水平值，趋势值分别为14250，1875，以及2018年四个季度的季节性因子，分别为0.7，0.98，0.56和1.75，那么就可以计算出2019年第1季度的水平值，趋势值，季节性数值和预测值，而α，β，γ值均为0.5，分别套入相应的公式。
（注：
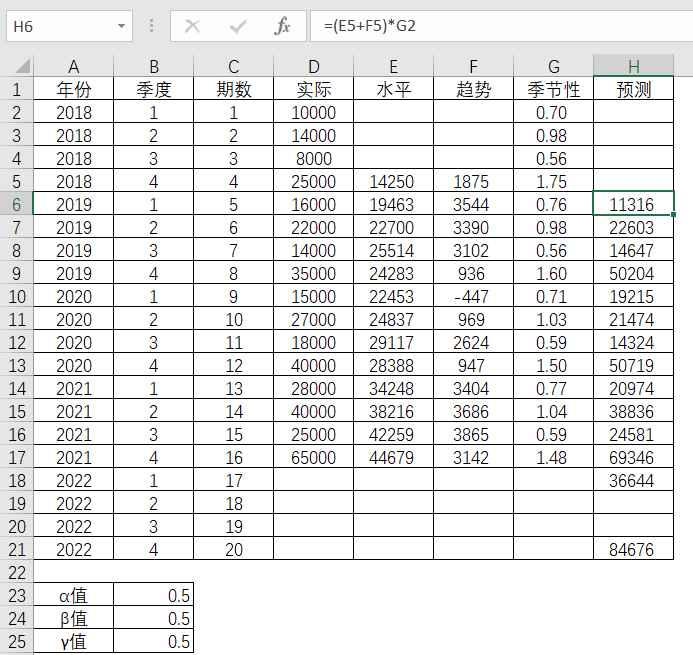
这样就得出了第5期（即2019年第1季度）的水平值为19463，趋势值为3544，季节性因子为0.76，预测值为11316，并如此类推，可以得到后续各期的水平值，趋势值和预测值。
在Excel处求得第5期的水平值
表4-19 Excel中水平值的求解
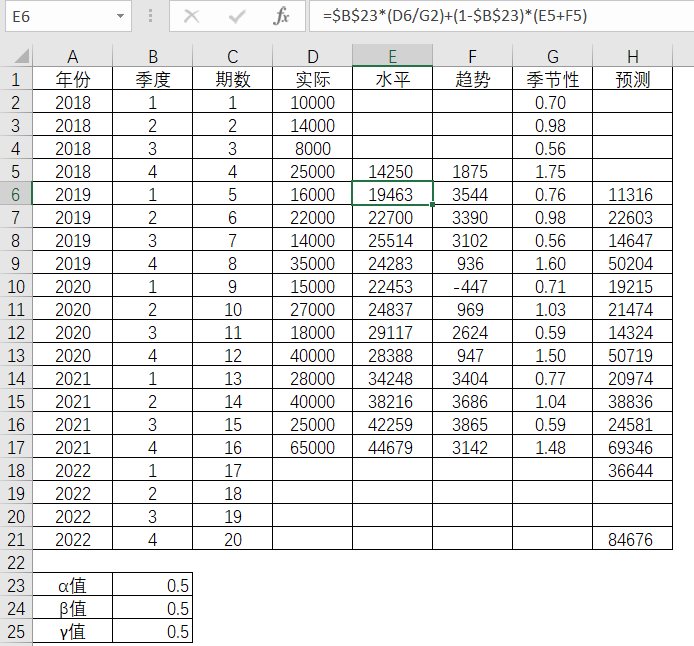
第5期的趋势值
表4-20 Excel中趋势值的求解
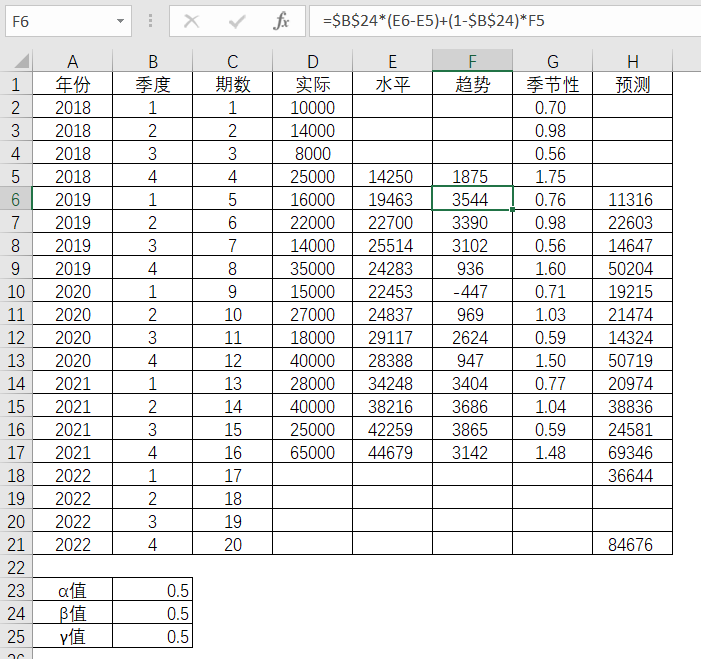
第5期的季节性因子
表4-21 Excel中季节性因子的求解
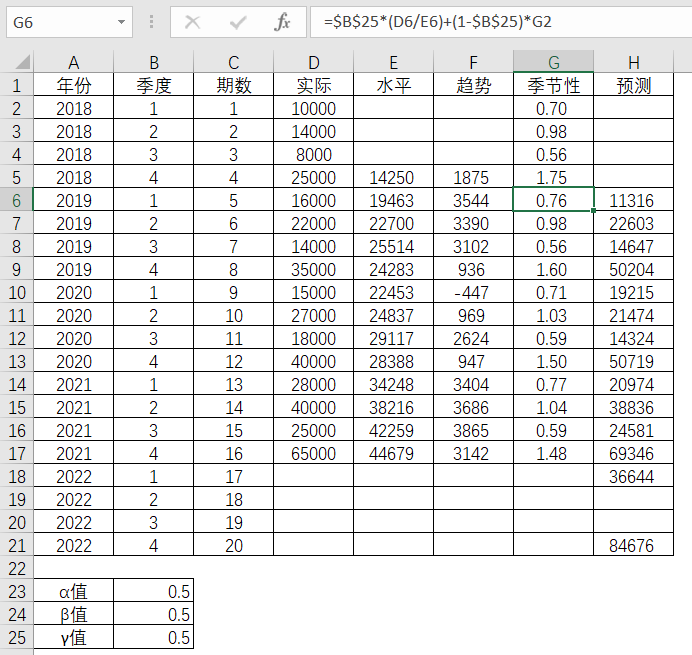
第5期的预测值
表4-22 Excel中预测值的求解
实际和预测的相应图示如下：
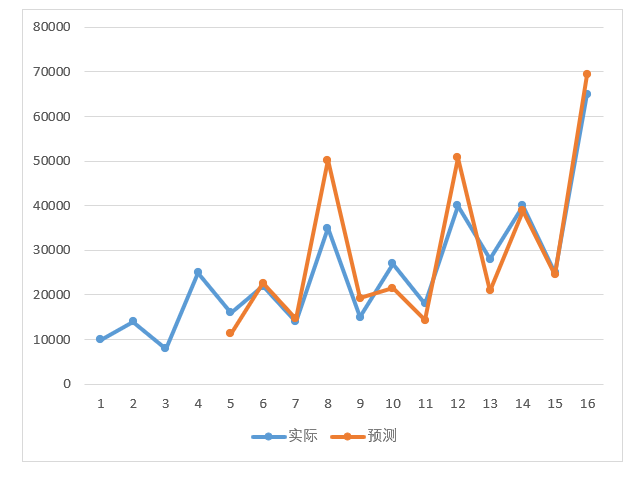
图4-19实际值和预测值的比较图
在知道16期的水平值，趋势值，季节性因子的情况下，也可以通过公式求得第20期（即2022年第4季度）的预测值。
通过第16期的数据来预测第20期，两者相差了4期，因此有4 X 3153的发生。而
表4-23 Excel中第20期预测值的求解
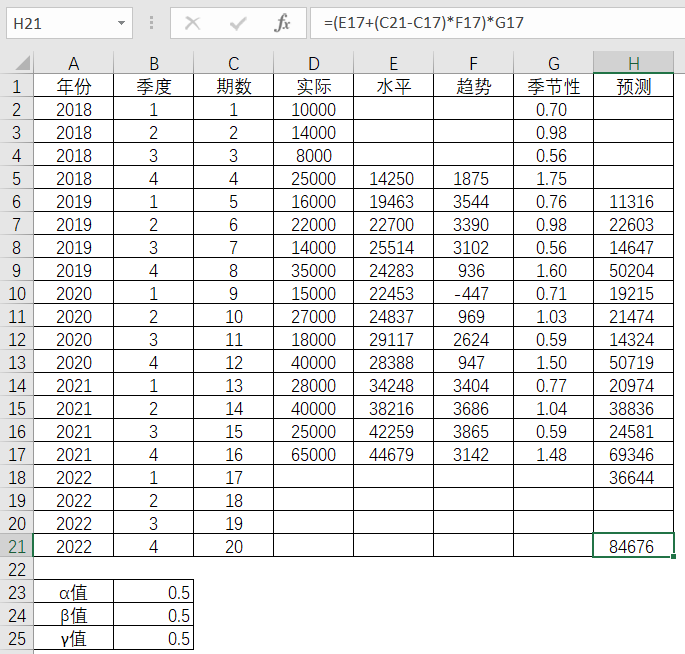
（注:Excel中由于涉及了小数点的计算，和上述公式计算的结果略有差异。）
加法模式公式：
n是期数
γ 是季节平滑常数，取值在0和1之间，读作Gamma
加法模式和乘法模式做法基本一样，都是确立初始值，数据也分为三个部分，即观测值，实验值和预测值。不过对待季节性部分，做法却不相同，乘法模式是当期的实际值和周期的平均值之比，得出季节性因子，而加法模式则是两者之差来得出季节性数值。那么2018年第1季度的季节性数值就是
表4-24 季节性数值求解
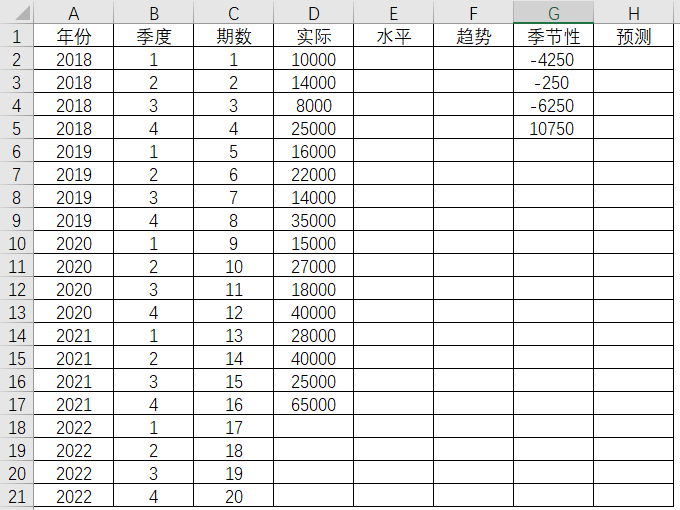
如此类推，得出2018年第1季度到第4季度的各季度季节性数值。由于2018年的全年数据作为观测值，那么水平值和趋势值初始值就是2018年的第4季度了。趋势值初始值为1875，而水平值可以根据当期的实际值，剔除季节性因素而得出，所以初始水平值就是当期实际值减去当期的季节性数值。2018年第4季度的季节性数值在之前计算得出为10750，那么2018年第4季度的水平值就是
而趋势值和乘法模式一样，由2019年的全年平均值和2018年的全年平均值的相比，再除以4个季度得出一个季度的值，就是视为2018年向2019年的趋势，并视为初始值。因此2018年第4季度的趋势值就是
得出了2018年第4季度的水平值，趋势值分别为14250，1875，以及2018年四个季度的季节性数值，分别为-4250，-250，-6250和10750，那么就可以计算出2019年第1季度的水平值，趋势值，季节性数值和预测值，而α，β，γ值分别为0.01，1和0.23，套入相应的公式。
（注：
这样就得出了第5期（即2019年第1季度）的水平值为16166，趋势值为1916，季节性指数为-3301，预测值为11875，并如此类推，可以得到后续各期的水平值，趋势值和预测值。
在Excel处求得第5期的水平值
表4-25 Excel中水平值的求解
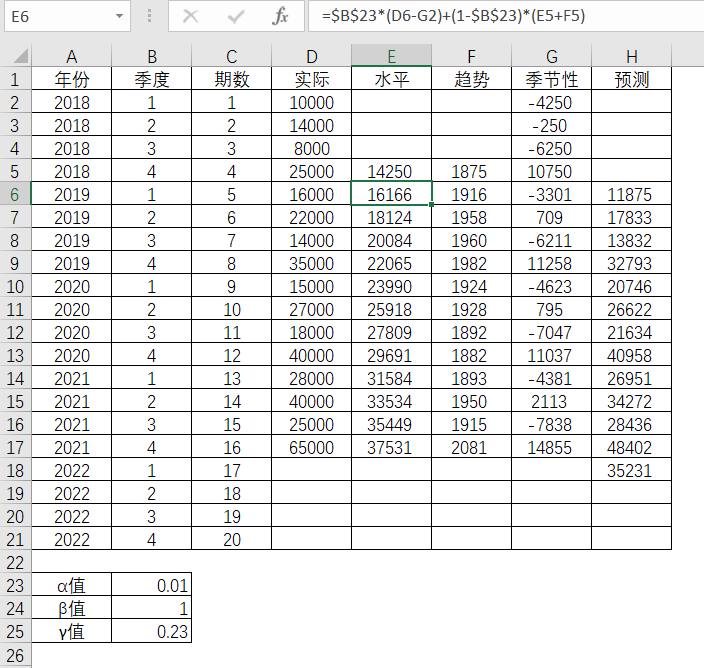
第5期的趋势值
表4-26 Excel中趋势值的求解
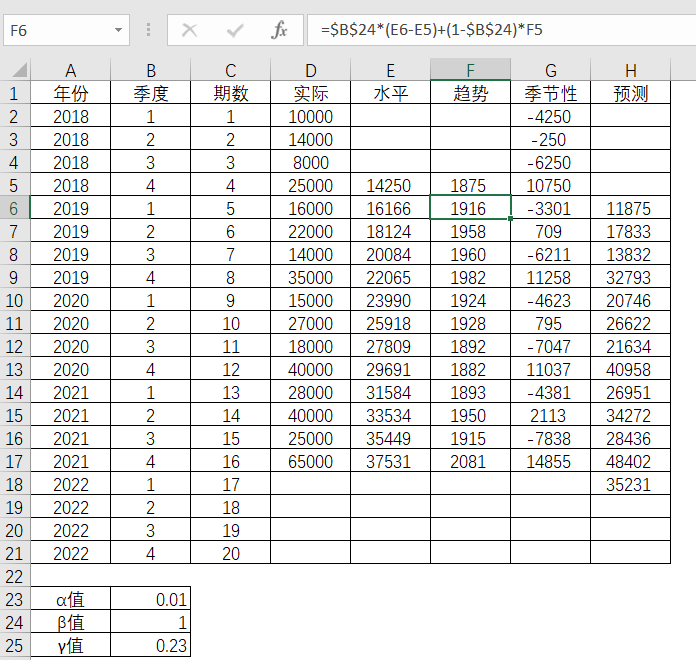
第5期的季节性数值
表4-27 Excel中季节性数值的求解
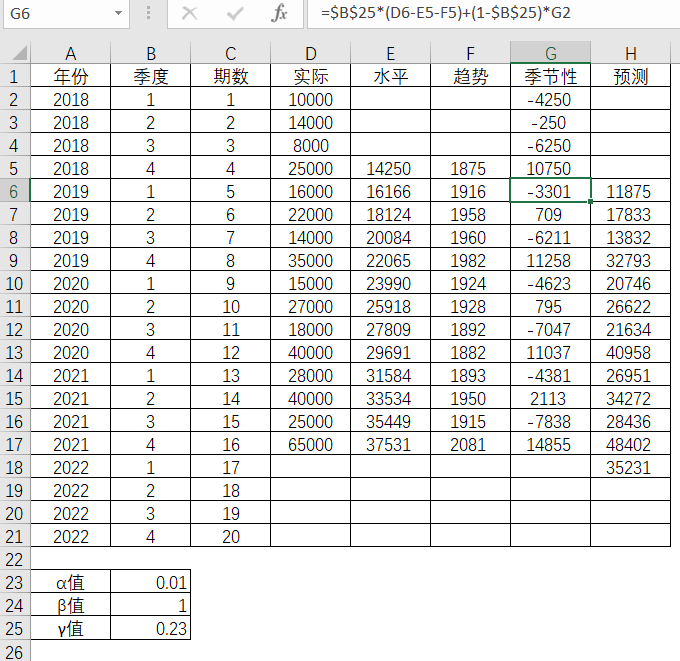
第5期的预测值
表4-28 Excel中预测值的求解
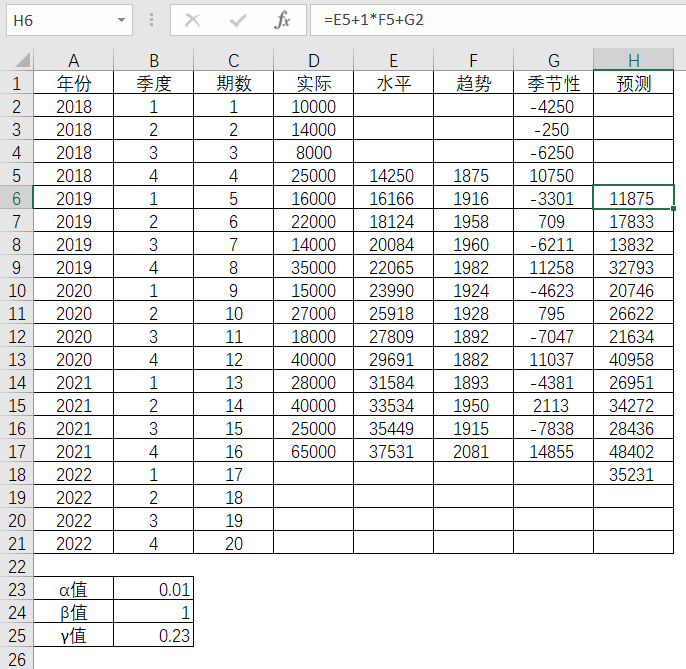
实际和预测的图示如下：
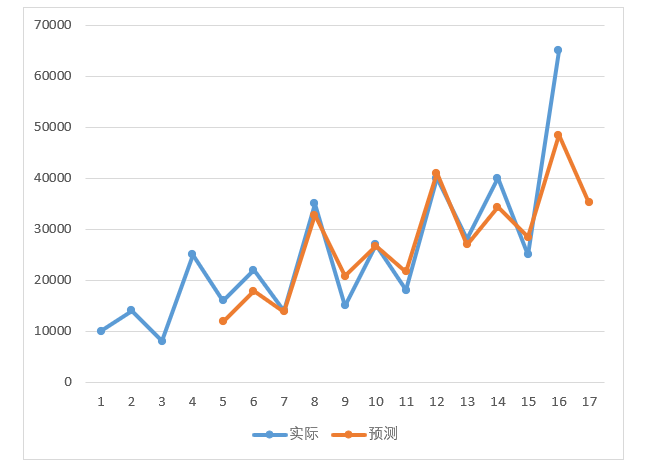
图4-20 实际值和预测值的比较图
在知道16期的水平值，趋势值，季节性数值的情况下，也可以通过公式求得第20期（即2022年第4季度）的预测值。
通过第16期的数据来预测第20期，两者相差了4期，因此有4 X 2081的发生。而
表4-29 Excel中第20期预测值求解
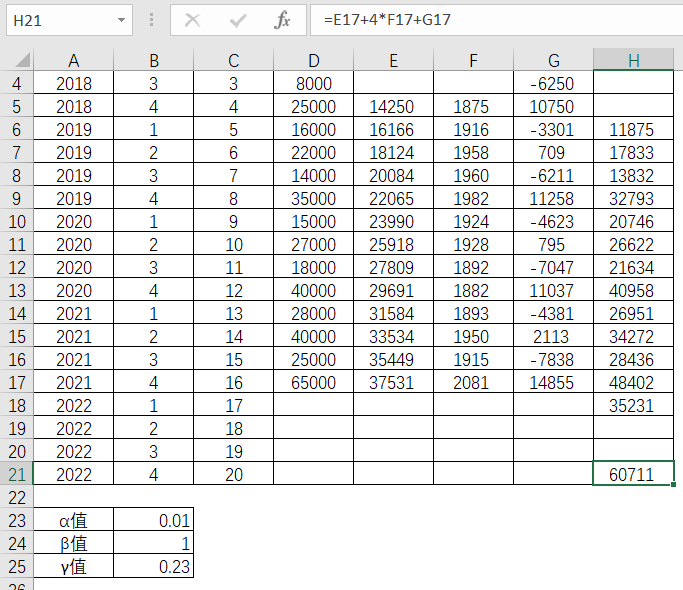
（注:Excel中由于涉及了小数点的计算，和上述公式计算的结果略有差异。）
同样地，三指数平滑法，不管是加法模式，抑或是乘法模式，也可以根据实际情况的需要，和单指数平滑法一样，在完成第一次指数平滑之后，可以继续进行第二次乃至更多次的指数平滑，从而得到最优效果。
【小插曲2】预测从清洗数据开始
清洗数据是预测的一个不可缺少的步骤。如果以百分比来划分预测工作的比重，那么说数据处理和清洗数据去到工作总量的80%也不为过。当数据整理好，以致数据规律都摸清，由此预测出来的结果就容易值得满意。
现今不少常用的预测方法都是时间序列法，也就是根据过去的历史数据，把隐藏的规律应用到未来的预测中。可以说，作为预测起点的数据，起着非常重要的作用。
清洗数据，大多数都会提到，诸如削峰填谷，减去季节性因素，又或者消除促销因素，然后再做预测。那么，到底为什么要清洗数据呢？
时间序列法的数据模型一般含有四个要素，分别为水平，趋势，季节性和噪声。因此所谓的数据清洗，就是要分析，整理出这四种因素，然后剔除并尽可能还原成水平状态。水平状态可以视为正常自然的需求产生，那么以水平状态使用时间序列分析技术，把相应的规律应用在未来的预测上，然后添加涉及的其他因素，诸如趋势，季节性因素，甚至一些涉及的可能随机因素或者市场行为。
从线条图4-21来看，可以视为如下发展。从还原后的水平，水平发展，再分别加入不同的因素。当然这个是思路图，不甚严谨，仅作参考。而所谓数据清洗，就是这个线图发展的逆向发展。
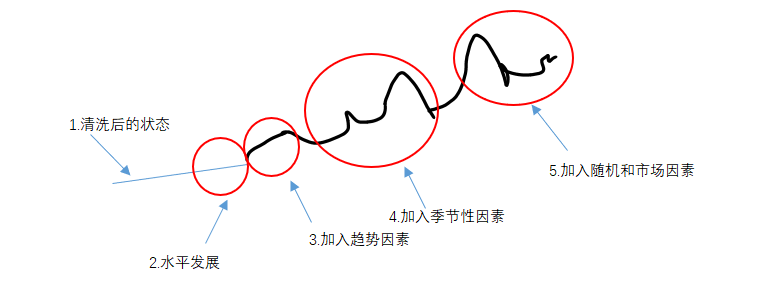
图4-21
在现实世界中数据清洗还要涉及更多的处理，比如缺失值，重复值，乃至分组，还有其他各式各样的不合理值，矛盾值等的处理。
当进行数据处理后，很多时候哪怕不进行各种方法进行预测，心里也多少摸到一定规律，对未来值有个大致的范围估计。
某电商近三年的销售数据，尽管三年的实际每年总需求，月均需求都各有不同，不过通过三年的比较可以看出，基本发展特点都比较相似，而且均含有上升趋势和季节性的特点。
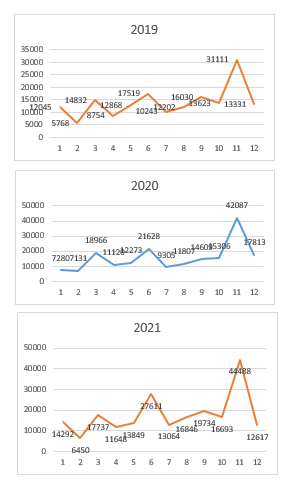
图4-22 某电商三年的月销售额
在这个基础上，该公司要对2022年1月进行预测，那么可以先行将数据清洗，分解出水平，趋势，季节性因素，然后预测2022年1月，接着加上相应的因素，得出模型并算出的预测值。
三年共36期的数据，每一年有12个月的数据，而季节性的因素是每12个月循环出现，比如3月，6月和11月都有明显的表现特征。
因此第一步，可以消除季节性和噪声的特征。移动平均是一个有效的方法，移动平均能把起伏的波动拉成相对平稳的状况，从而某种程度上，去到“削峰填谷”的作用，减少季节性带来的波动。根据观察，每12个月都会出现雷同的波动情况，那么以12个月为一个周期进行计算水平估计值。
以中间点为计算开始点，即从6月开始移动平均：
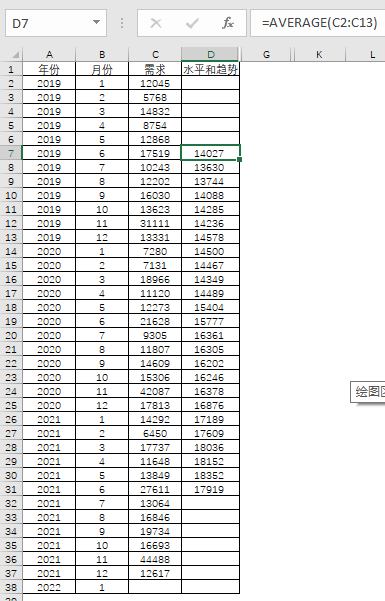
表4-30
选择6月，是因为处于中间点。如果选择12月，那么将12个月的平均值从12月开始计算，那么对于这个月来说，大部分都是“陈旧”的数据，对水平的估计代表性有所降低，反之如果选择1月，参与的数据都是较新的数据，又是另外一个极端。选择6月作为移动平均的起点，作为水平的估计值，既可以消除噪声，同时去除季节性的波动。
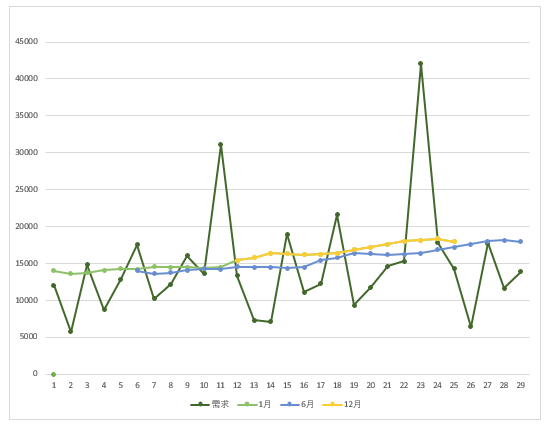
图4-23 不同采用月份的比较
根据图，三年的趋势是上升且有季节性波动，如果采用2019年1月作为计算起点，那么趋势上升就会加快，出现在11期（2019年11月），反之采用2019年的12月，数据反应表现滞后，在24期（2020年12月）才有出现趋势上升。因此选择2019年6月这个中心做移动平均，表现适中。
需求包含了水平，趋势，季节性和噪声，通过移动平均，去除了噪声和季节性后，剩下的就是水平和趋势。然后减去趋势，剩下的就是水平的估计值了。
趋势是本期和上一期发展的对比变化，不断地一期又一期数据累计。因此，最简单的方法就是上一期减去本期数据，就得一期的趋势变化，如此类推。那么就分解出其中一个因素：趋势。
得出2021年6月的趋势是-433，那么后续的就以这个最新的趋势进行类推，2021年7月就是第一期的-433，即-433 * 1= -433 ，假如要推测2022年1月的，类推就是7期的数据，即-433 * 7= -3031
表4-31 趋势的计算
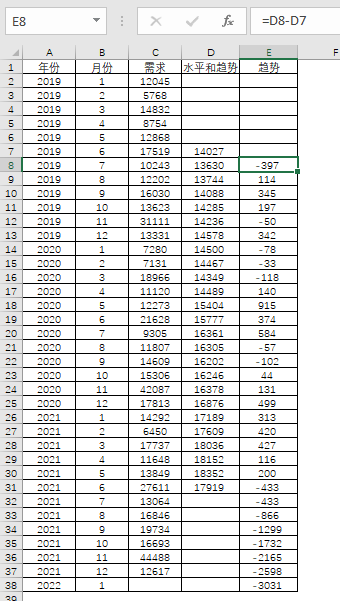
同理，需求减去已经得知的水平和趋势后，就是噪声和季节性。
表4-32 噪声和季节性的计算
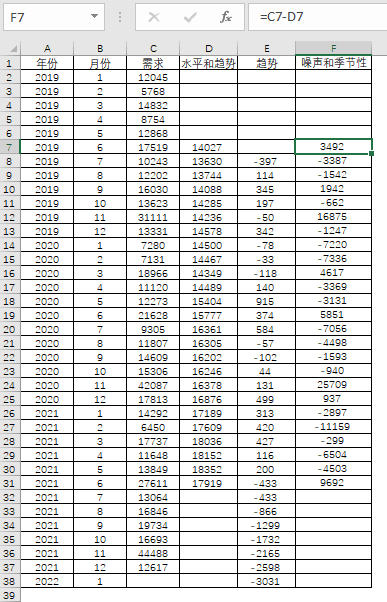
最后一步就是，拆分出季节性，就可以完整地得出各个因素了。由于季节性是每12个月重复出现，那么最简单直接的方法也是有效的，就是取平均值。因为一年中的每一个月都代表不同的季节性，取每年的1月平均值作为1月的估值，同理，2月如此。这个是加法的季节性调整，当然可以还有一种是乘法的季节性指数，就是对应的月份和平均值的比例，这个电商另行计算测试，经比较，讨论和分析，最终还是选择加法的季节性指数。
表4-33
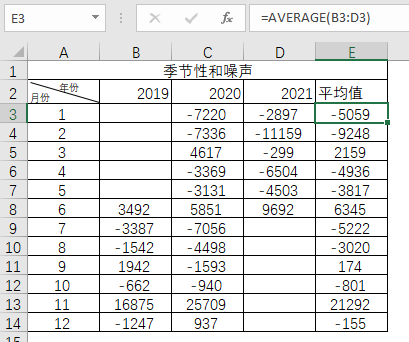
通过图4-47的计算，得出每个月的均值之后，加入在季节性因素中。
表4-34
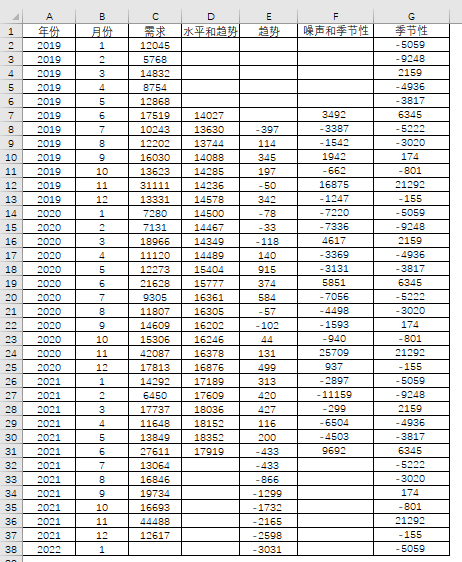
如此一来，得到的最新数据有，最新的水平和趋势值（2021年6月为17919），最新的趋势，2022年1月的值为-3031，还有1月的季节性值，是-5059。
得出清洗后的数据，相关人员还不忘检查一遍，避免犯上其他公司的常见错误：就是把历史销售数据假设成为历史需求数据。当销售不能满足需求，出现缺货等现象，这个历史销售就不能等同于历史需求数据了。还有其他诸如促销，市场和竞争对手行为等，都会对真实的需求造成影响。而这些工作并不能简单通过数据的治理完成，这个时候，相关人员还要联同市场部门，销售部门等对细节确认，尽可能把“脏”数据清洗出来。
当清洗数据确认完毕后，接下来就要预测2022年的数值。
表4-35
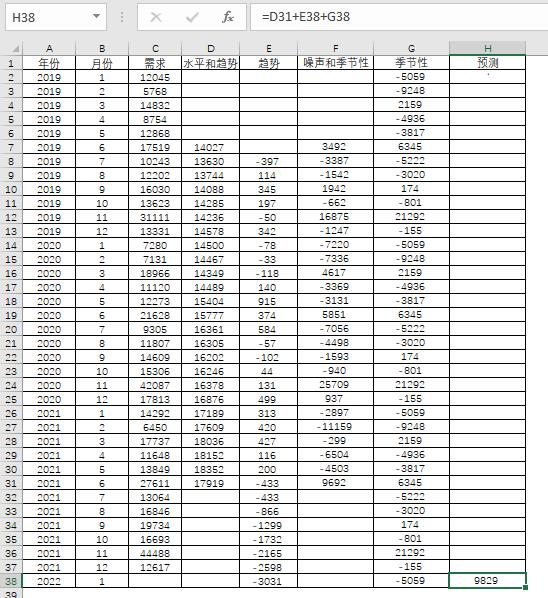
得出的2022年1月预测值为9829，包含了水平，趋势和季节性因素，当然，这不会包含随机因素，即噪声。
通过数据规律，每年的12月到次年的1月，需求有一定的下滑出现，那么预测出来的值也含有雷同的规律。
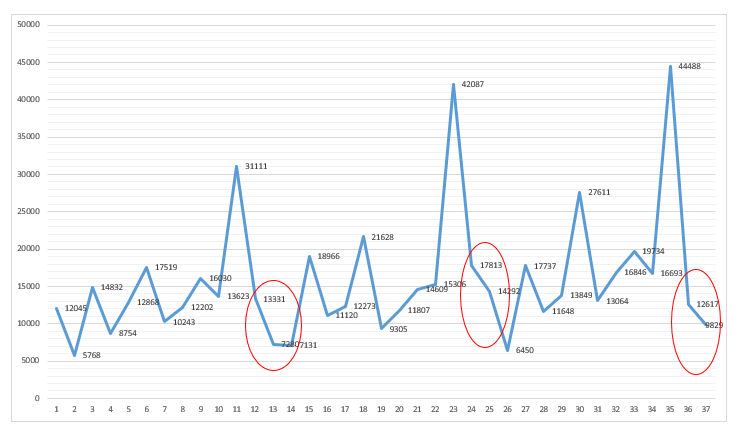
图4-24
某电商通过数据清洗，分解出不同因素后，从而利用简单的方法对下一期的需求进行预测。
