四分位数是指把一组数据由小到大排序后，分成四等份，处于三个分割点位置的数值就是四分位数。

四分位划分的用处就是将一批数据一分为四，寻找出起主要作用的数值。而最小的四分位数称呼为下四分位数，而最大的四分位数则称为上四分数，中间的四分位数则是中位数。而四分位距则有助于清楚知道处于中心部分的50%的数据是如何。通过这个，把异常值，极大值和极小值排除在外。

四分位距=上四分位数-下四分位数。它是50%中间值形成的一个间距。

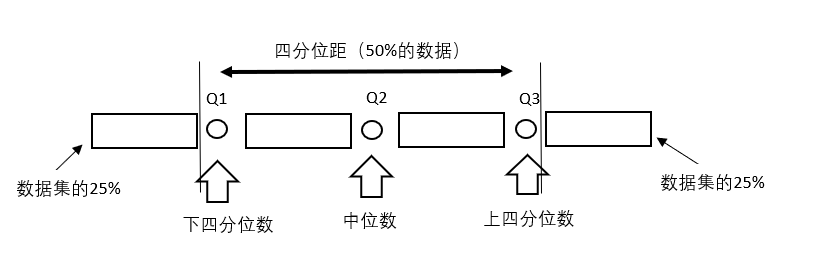
图3-3 四分位数

关注四分位距的优点，就是减少异常值的影响。在上四分分数以上的25%数据，以及下四分位以下的25%，包含了数据中的极大值和极小值，因此当仅仅关注四分位距，即中位数附近的数值，那么就会剔除这些包含了极大值和极小值的异常值，从而得到一个不会比异常值扭曲结果的观察方法。

爱美斯乐集团这些日子准备挑选一批高个子，准备拍摄一组宣传照片，借此推广公司的产品。产品的亮点要建立在阳光形象上，匹配在身材高大的模特上，会让每个观看过这个广告照的人，都在心里留下印象。当然，要是模特本身具备相当的人气，那自然会带来更好的效果。很快，8位高个子模特最终被选为候选人，他们身高均在1.88米到1.93米之间。这队模特一排而立，颇具吸引力。

图3-4（图片来源于网络）

不过，很快有人提议并表示能够很大程度，说服姚明加入这个队列。然而姚明若要加入的话，他那2.23米的身高就显得特别碍眼。原本差不多的身高高度，因为高大的姚明加入，导致出现了非常大的不一致。

图3-5（图片来源于网络）

与此同时，从增加广告话题性和效果来看，也因此有人提议邀请被誉为苏神的苏炳添加入，作为首位进入奥运百米男子短跑决赛的黄种人，苏炳添身高只不过是1.72米，和广告计划的一队高个模特并不完美吻合，不过由于姚明加入，总体的高度来说，依然是一队高个子模特。不过这样一来，这队模特的身高变得更加参差不齐，视觉效果打了折扣。

图3-6

为此反复讨论，最终不得不拒绝姚明和苏炳添的加入想法。那8位身高1.9米的模特而言，苏炳添和姚明的身高就是一个异常值。本来8位身高差不多的模特，平均值和中位值就在1.9米左右，苏炳添和姚明的加入让数据产生了扭曲，并带来身高落差的视觉效果，最终还是剔除这些包含了极大值和极小值的异常值，仅仅保留那8位1.9米左右的模特会变得更好。这8位模特的身高值都是中位数值附近的，是出于数据集中心的50%左右的数据。同时，广告的本身聚焦点放在产品身上，而非两大人气者——苏炳添和姚明的身上。

最终，广告商打消了邀请苏炳添和姚明加入的想法。

四分位分类，对于认识货物特征有着重要的辅助作用。华尔公司就是通过四分位分类来提升货物特征的认识。

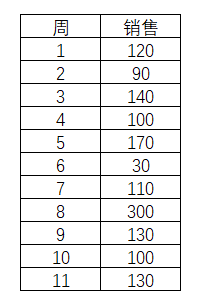
华尔公司的第1周到第11周的销售数据。计算出来的均值是129个单位。

表3-7

很多时候当不考虑太复杂的情况，一般设定库存计划，都是简单地用提前期乘以该期内的平均销售期来确立一个安全库存量，从而覆盖提前期不确定性带来的影响。而一旦适用了因为异常值而扭曲了的均值，库存量势必增大，极大可能损害库存管理的健康程度。

该公司的供货提前期是8天，那么按照提前期乘以平均销量，8 X129 = 1032 ，因此他们需要做库存计划，设立1032个安全库存量。

不过，当把这个销售数据转换成图3-9观察，发现其中有2个值是非常值得留意的。图中两个圆圈所圈着的数值，和其他数值相比，比较偏离。从这堆数据来说，这2个值可以视为异常值。

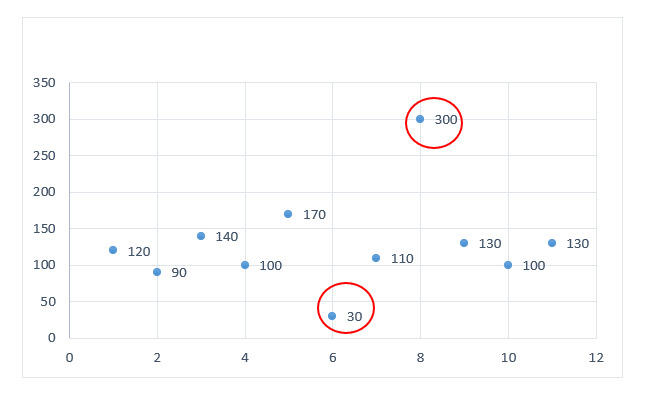
图3-7

根据这组数据特征，就要审视一下这两个异常值是怎么回事。如果能幸运地分析到具体原因造成这些销售数字的差异，比如是品牌联动带来的影响，如优衣库和KAWS联名T恤造成抢买这类情况导致销售大增，又或者异常事件导致突然的销售下滑，比如新疆棉问题导致某些牌子被罢买，那么可以根据实际分析得到的情况，看这个数字是否小概率事件而决定是否引入计算当中。

剔除异常值，找出四分位值，可以利用Excel函数计算。先通过函数MIN , MAX , MEDIAN分别计算出最小值，最大值和中位数值。

表3-8 最小值的Excel计算

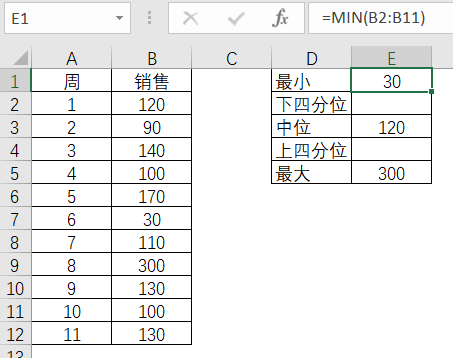
表3-9 中位数的Excel计算

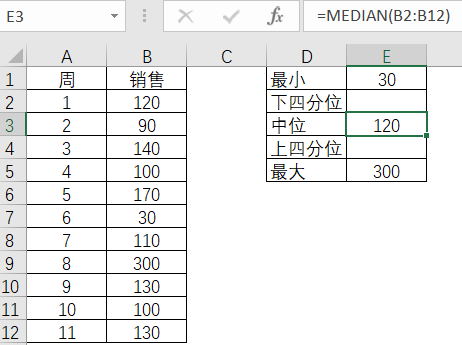
表3-10 最大值的Excel计算

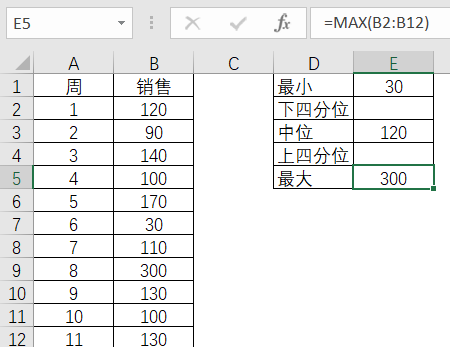
然后再通过函数QUARTILE,INC来计算出上下四分位数。

表3-11 下四分位的Excel计算

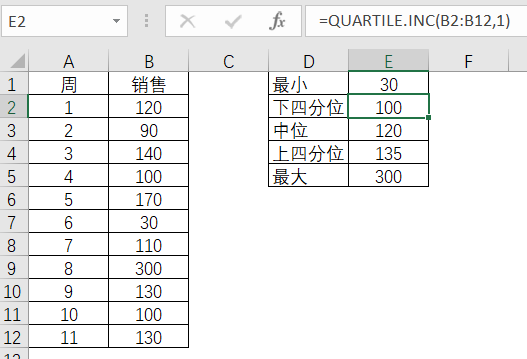
表3-12 上四分位的Excel计算

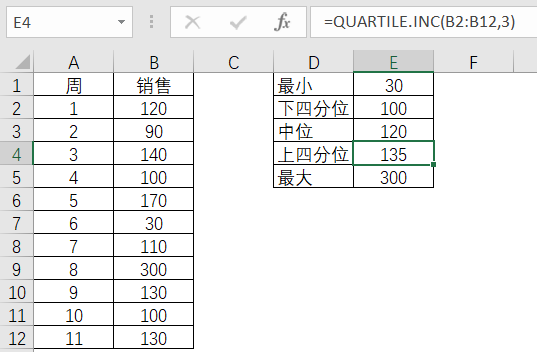
图3-14函数中的B2:B13后面数字的1和3表示第一个四分位点（即1/4）和第三个四分位点（3/4），四分位距则是 135- 100 = 35 ，从而可以知道50%的销售数字都在这35的距离里波动。

上下四分位内的平均值是118 ，如果使用公式计算8天提前期的库存量，则 8 X 118 = 944个单位。944个单位的库存量比起之前并没有剔除异常值而计算的1032少了88个单位，下降了8%的库存量。

通过四分位法有助于结果不被异常值扭曲，而不容易造成被均值带来扭曲而欺骗。

特别是在XYZ分析法，假如变异系数设立在0.5为分界点，并借此分出X和Y 类，那么0.53或者0.55就被分入Y类的，这些接近X类的货物，非常有可能是由于少数的异常值导致波动增大而不归入X类。因此这些异常值就欺骗了我们，从而不能正确认识这个货的特征，造成选择了并非最恰当的预测或者库存计划方法。通过四分位法，有助于减少异常值带来的问题，避免把本应该是X类货物错误地分类到Y类上。

四分位法还可以用在多个方面，比如提前期的计算等等。

此外，四分位还可以根据其原理，把数据分成十份，而不是四分，就是十分位了。使得每一个数据块包含了10%的数据，而起分分割作用的数值就称为十分位数。而分成一百份，起分割作用的数值就称为百分位数了。

根据实际的情况，除了选用四分位法，还可以扩展适用十分位法，百分位法等。